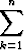Homogeenisen yhtälön ratkaisujoukko

Kertalukua n oleva lineaarinen ja homogeeninen differentiaaliyhtälö on normaalimuodossa

y⁽ⁿ⁾ + P_n-1(x)y^(n-1) + . . . + P₁(x)y' + P₀(x)y = 0.

Funktiot P_k oletetaan jatkuviksi tarkasteluvälillä. Yhtälön yleisen ratkaisun voidaan osoittaa olevan muotoa

y = 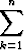C_ky_k  eli  y(x) = C₁y₁(x) + C₂y₂(x) + . . . + C_ny_n(x),

missä C₁ ,  C₂ ,  . . . ,  C_n ovat määräämättömät vakiot ja funktiot y₁(x),  y₂(x),  . . . ,  y_n(x) ovat mitkä tahansa lineaarisesti riippumattomat yhtälön yksittäisratkaisut.

Homogeeniyhtälön lineaarisesti riippumattomia yksittäisratkaisuja sanotaan sen perusratkaisuiksi ja niiden sanotaan muodostavan ratkaisujen perusjärjestelmän.

Yleisen ratkaisun muoto ei anna viitteitä siitä, miten ratkaisu voitaisiin löytää. Yleistä algoritmia ratkaisun etsimiseen ei edes ole.

Jos kyseessä kuitenkin on ensimmäisen kertaluvun yhtälö y' + P₀(x)y = 0, yleinen ratkaisu löydetään separoimalla. Tämä johtaa muotoon y(x) = C₁y₁(x), mikä vastaa em. yleistä muotoa tilanteessa, missä summassa on vain yksi termi.

On helppoa todistaa, että väitetyn muotoinen lauseke todella on differentiaaliyhtälön ratkaisu. Tämä tapahtuu helpoimmin lausumalla yhtälö lineaarisen differentiaalioperaattorin L avulla muodossa Ly = 0 ja sijoittamalla lauseke tähän:

L(C₁ y₁ + C₂y₂ + . . . + C_ny_n) = C₁Ly₁ + C₂Ly₂ + . . . + C_nLy_n = 0.

Tuloksena on 0, koska jokainen y_k on differentiaaliyhtälön yksittäisratkaisu eli Ly_k = 0.

Hieman vaikeampaa on osoittaa, että yhtälön kaikki ratkaisut voidaan kirjoittaa tähän muotoon valitsemalla vakioille C_k sopivat arvot. Tämä perustuu keskeisesti ratkaisujen Wronskin determinantin ominaisuuksiin ja yleiseen lauseeseen alkuarvoprobleeman ratkaisun yksikäsitteisyydestä.