| prvdyh.mws |
Olkoon annettuna käyräparvi
> kayraparvi:= (x+_C1)^2+(y+_C2)^2=_C3^2;
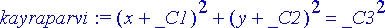
missä _ C1 , _ C2 ja _ C3 ovat parven parametrit. Jokaisella (ainakin lähes) näiden arvokombinaatiolla parvesta saatava yhtälö esittää tason ympyrää. Toisaalta tason jokaisen ympyrän yhtälö on tätä muotoa.
Tulkitaan y funktioksi muuttujasta x tavoitteena löytää differentiaaliyhtälö tälle funktiolle:
> parvi:= subs(y=y(x), kayraparvi);
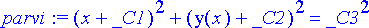
Derivoidaan tämä yhtälö kolmesti, minkä jälkeen saaduista neljästä yhtälöstä eliminoidaan parametrit _ C1 , _ C2 ja _ C3 :
> parvi1:=diff(parvi, x);
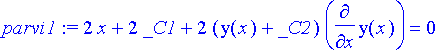
> parvi2:=diff(parvi, x$2);
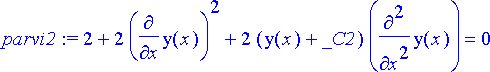
> parvi3:=diff(parvi, x$3);
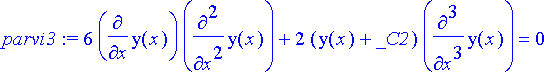
> ratk:= eliminate({parvi, parvi1, parvi2, parvi3}, {_C1, _C2, _C3});
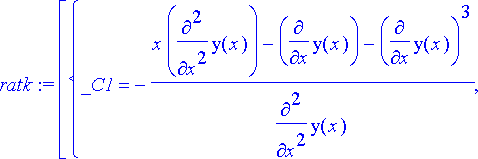
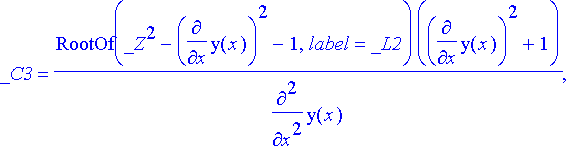
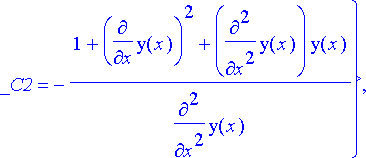
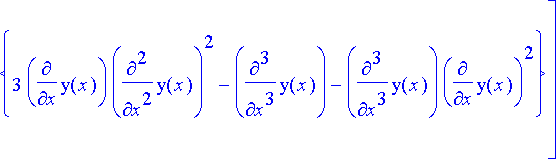
Eliminate -komento antaa listan, jonka viimeisenä alkiona on eliminoinnin tulos polynomin muodossa. Ratkaisu muunnetaan yhtälömuotoon merkitsemällä polynomi nollaksi.
> diffyht:= op(ratk[-1])=0;
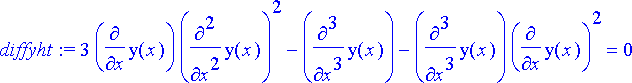
Tuloksena on kolmannen kertaluvun differentiaaliyhtälö, jonka yleisenä ratkaisuna on alkuperäinen käyräparvi. Kyseessä on siten kaikkien tason ympyröiden differentiaaliyhtälö.
Saadulla differentiaaliyhtälöllä on kuitenkin muitakin ratkaisuja:
> simplify(subs(y(x)=_D1*x+_D2, diffyht));
