Esimerkit : Separoituvat ja niihin palautuvat yhtälöt

Kolmannen kertaluvun yhtälön palauttaminen ensimmäiseen kertalukuun ja ratkaiseminen separoimalla

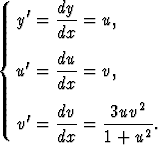
Kolmannen kertaluvun autonomista yhtälöä y'''(1 + y'2) = 3y'y''2 vastaa normaaliryhmä

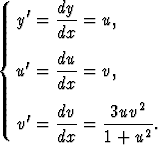
dy y'= ---= u, dx { ' du u = ---= v, dx ' dv- -3uv2-- v = dx = 1 + u2 .

Kun kolmas yhtälö puolittain jaetaan toisella, saadaan vain muuttujista u ja v riippuva ensimmäisen kertaluvun yhtälö:

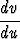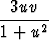dv- du = -3uv--- 1 + u2.

Tämä on separoituva ja sen ratkaisu voidaan saattaa muotoon

v = C1(1 + u2)3/2.

Kyseessä on differentiaaliyhtälön ensimmäinen integraali.

Normaaliryhmän toisen yhtälön mukaan on

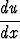du --- dx = C1(1 + u2)3/2,

mikä jälleen on separoituva yhtälö. Separointi ja puolittainen integrointi antavat

C1x + C2 = 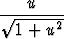u V~ ------- 1 + u2,

jolloin

u2 = 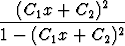(C1x + C2)2 1---(C--x-+-C--)2- 1 2.

On saatu differentiaaliyhtälön toinen integraali.

Normaaliryhmän ensimmäinen yhtälö antaa nyt

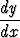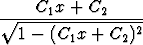dy- dx = ----C1x--+-C2----- V~ 1---(C-x-+-C--)2 1 2,

joten ratkaisu saadaan yhdellä integroinnilla:

y = -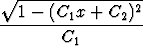 V~ ---------------- --1---(C1x-+--C2)2 C1 - C3- C1.

Integroimisvakio on kirjoitettu muotoon -C3/C1, mikä saa kaikki reaaliarvot C3:n arvon vaihdellessa, ts. valinta ei rajoita vakion arvoja. Tulos voidaan kirjoittaa symmetriseen muotoon

(C1x + C2)2 + (C1y + C3)2 = 1.

Tätä voidaan kutsua differentiaaliyhtälön kolmanneksi integraaliksi.

Jakamalla yhtälö luvulla C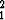2 1 ja merkitsemällä D1 = C2/C1, D2 = C3/C1, D3 = 1/C1 päädytään muotoon

(x + D1)2 + (y + D2)2 = D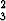2 3.

Tämä osoittaa, että kyseessä on tason kaikkien ympyröiden muodostama käyräparvi ja alkuperäinen differentiaaliyhtälö on siis tämän käyräparven differentiaaliyhtälö.

Lukija pohtikoon, mitä tapahtuu, jos C1 = 0. Millaisia ratkaisuja tämä antaa yhtälölle?

Ratkaiseminen: palauttaminen ensimmäiseen kertalukuun
Ratkaiseminen: separoituva yhtälö
Teoria: normaaliryhmä
Teoria: käyräparvi ja differentiaaliyhtälö
Esimerkki: käyräparven differentiaaliyhtälön etsiminen
SKK 15.5.2001