| F2 | (x, y, y', y'', C1, C2, . . . , Cn) = 0, | ||
| F3 | (x, y, y', y'', y''', C1, C2, . . . , Cn) = 0, | ||
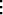 | |||
| Fn | (x, y, y', y'', . . . , y(n), C1, C2, . . . , Cn) = 0. |
Differentiaaliyhtälön yleinen ratkaisu voidaan ajatella käyräparveksi. Kun yleisen ratkaisun määräämättömille vakioille annetaan arvot, saadaan jokin parveen kuuluva käyrä. Määräämättömät vakiot ovat siten käyräparven kannalta sen parametreja. Jokaista (sallittua) parametrien arvokombinaatiota vastaa tietty käyrä ja kääntäen.
Differentiaaliyhtälön ratkaiseminen tarkoittaa tällöin vastaavan käyräparven etsimistä. Käänteinen tehtävä on muodostaa annetulle käyräparvelle sitä vastaava differentiaaliyhtälö.
Periaatteessa tämä tapahtuu seuraavasti:
Käyräparven yhtälö on muotoa
F0(x, y, C1, C2, . . . , Cn) = 0,
missä C1 , C2 , . . . ovat parven parametreja. Jos tässä yhtälössä y ajatellaan funktioksi y(x) ja yhtälö derivoidaan muuttujan x suhteen, saadaan periaatteessa muotoa
F1(x, y, y', C1, C2, . . . , Cn) = 0
oleva yhtälö. Derivoimalla tätä edelleen saadaan uusia vastaavan tyyppisiä yhtälöitä, mutta jokaisessa esiintyy yhtä kertalukua korkeampi derivaatta:
| F2 | (x, y, y', y'', C1, C2, . . . , Cn) = 0, | ||
| F3 | (x, y, y', y'', y''', C1, C2, . . . , Cn) = 0, | ||
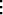 | |||
| Fn | (x, y, y', y'', . . . , y(n), C1, C2, . . . , Cn) = 0. |
G(x, y, y', . . . , y(n)) = 0,
ts. kertalukua n oleva differentiaaliyhtälö.
Eliminointi voi tapahtua ratkaisemalla jokin yhtälö jonkin parametrin suhteen ja sijoittamalla tämän lauseke muihin yhtälöihin. Tällöin parametrien ja samalla yhtälöiden määrä vähenee yhdellä. Toistamalla askel n kertaa saadaan kaikki parametrit eliminoiduiksi ja jäljelle jää yksi yhtälö.
Toisaalta symbolisista laskentaohjelmista löytyy yleensä valmiit komennot tämäntyyppisiin eliminointeihin.
Jos käyräparven yhtälö on algebrallisesti liian monimutkainen tai sisältää transkendenttifunktioita, ei eliminointi useinkaan onnistu.