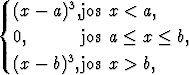 missä a < 0 < b,
missä a < 0 < b,
Differentiaaliyhtälö y' = 3y2/3 on separoituva, ja tällä tavoin sen ratkaisuksi saadaan
y = (x + C)3.
Alkuehtoa y(0) = 0 vastaava ratkaisu näyttäisi olevan y = x3.
Alkuehdon täyttäviä ratkaisuja on kuitenkin muitakin. Yhtälön ensinnäkin selvästi toteuttaa identtisesti häviävä funktio: y(x) = 0 kaikilla x. Myös paloittain määritelty funktio
y(x) = 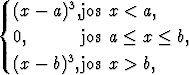 missä a < 0 < b,
missä a < 0 < b,
on alkuarvoprobleeman ratkaisu, sillä funktio on kaikkialla derivoituva ja toteuttaa sekä differentiaaliyhtälön että alkuehdon. Alkuehdon toteuttavia ratkaisuja on siten äärettömän paljon.
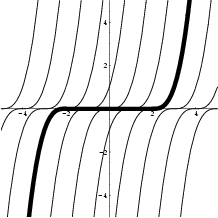
Differentiaaliyhtälön oikean puolen funktio f(x, y) = 3y2/3 on kaikkialla jatkuva, mutta sen osittaisderivaatta
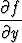 =
= 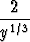
ei ole määritelty x-akselilla eikä sitä voida määritelläkään siten, että siitä tulisi jatkuva. Alkuarvoprobleeman ratkaisun yksikäsitteisyyttä koskevan lauseen oletukset eivät siten toteudu.