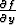Ratkaisun olemassaolo ja yksikäsitteisyys

Keskeinen kysymys alkuarvoprobleeman

y' = f(x, y),   y(x₀) = y₀

tutkimisessa on, millä edellytyksillä probleemalla toisaalta on ratkaisu ja toisaalta näitä ei ole enempää kuin yksi. Ratkaisulla tarkoitetaan tällöin jossakin pisteen x₀ ympäristössä derivoituvaa, yhtälön ja alkuehdon toteuttavaa funktiota riippumatta siitä, onko tämä lausuttavissa alkeisfunktioiden avulla tai löydettävissä jollakin integrointimenettelyllä.

Ratkaisun olemassaoloa ja yksikäsitteisyyttä koskeva päätulos on seuraava:

Lause. Funktio f ja sen osittaisderivaatta 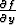olkoot jatkuvia suorakulmiossa {(x, y) | |x - x₀| < a,  |y - y₀| < b}. Tällöin on olemassa väli ]x₀ - h, x₀ + h[ siten, että alkuarvoprobleemalla

y' = f(x, y),   y(x₀) = y₀

on yksikäsitteinen ratkaisu y(x) tällä välillä.

Väli ]x₀ - h, x₀ + h[ on muuttujan x vaihteluvälin [x₀ - a, x₀ + a] osaväli ja voi olla tätä huomattavastikin suppeampi.

Lauseen todistuksen pohjana on alkuarvoprobleemaa vastaavasta integraaliyhtälöstä

y(x) = y₀ + 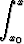f(x, y(x)) dx.

muodostettu rekursiokaava

y_n+1(x) = y₀ + 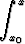f(x, y_n(x)) dx.

Käyttämällä lähtöfunktiona esimerkiksi vakiofunktiota y₀(x) = y₀ (= alkuehdossa annettu arvo) muodostetaan rekursion avulla jono alkuehdon toteuttavia funktioita: y₀ (x),  y₁ (x),  y₂(x),  . . . . Tämä jono osoitetaan suppenevaksi, jolloin sillä on rajafunktio olemassa. Rajafunktion voidaan osoittaa toteuttavan sekä differentiaaliyhtälön että alkuehdon. Lopuksi on vielä osoitettava ratkaisun yksikäsitteisyys, ts. näytettävä, että jos sekä y(x) että z(x) ovat alkuarvoprobleeman ratkaisuja, nämä ovat samat.

Esitetyssä muodossa lause koskee vain ensimmäisen kertaluvun differentiaaliyhtälöitä. Täysin vastaavalla tavalla voidaan kuitenkin todistaa kertalukua n olevan alkuarvoprobleeman ratkaisua koskeva lause, kun differentiaaliyhtälö korvataan vektorimuotoisella normaaliryhmällä Y ' = F (x, Y ) ja alkuehto kirjoitetaan muotoon

Y (x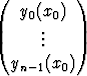₀) = = = Y₀.

Todistukseen tarvitaan vain vähäisiä merkinnällisiä muutoksia, lähinnä itseisarvomerkkien korvaamisia vektorin normilla.

Lause esietään usein hieman vahvemmassa muodossa, jossa funktion f osittaisderivaatan 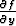olemassaoloa ei tarvitse olettaa. Tällöin oletetaan, että funktio f toteuttaa lauseessa mainitussa suorakulmiossa ns. tasaisen Lipschitzin ehdon |f(x, y) - f(x, z)| < L|y - z|, missä L on positiivinen vakio.

Tämän tyyppinen ehto on kuitenkin oleellinen: Vastaesimerkillä on mahdollista osoittaa, että lause ei päde, jos ehdosta luovutaan.