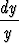Ensimmäisen kertaluvun lineaarinen ja homogeeninen yhtälö

Ensimmäisen kertaluvun normaalimuotoinen homogeeniyhtälö on y' + P₀(x)y = 0, missä kerroinfunktio P₀(x) oletetaan jatkuvaksi tarkasteluvälillä.

Kyseessä on separoituva yhtälö

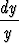= -P₀(x) dx,

jonka puolittainen integrointi johtaa yleiseen ratkaisuun

y = Ce^{-P₀(x) dx}.

Integroitaessa tarvittava vakio on aluksi kirjoitettu muotoon ln |C|. Tästä huolimatta myös arvo C = 0 on mahdollinen, ts. y = 0 kaikilla x, kuten nähdään suoraan alkuperäisestä yhtälöstä.

Jos on annettu alkuehto y(x₀) = y₀, voidaan puolittainen integrointi tehdä määrättynä integraalina:

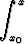
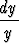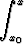= -P₀(x) dx.

Tällöin ratkaisu saa muodon

y = y₀ e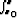^{-P₀(x) dx}.

Ratkaisun periaatteellinen muoto on y = Cy₁(x), missä y₁(x) tarkoittaa mitä tahansa nollafunktiosta eroavaa (ts. lineaarisesti riippumatonta) yhtälön yksittäisratkaisua.