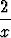 y = x2 cos 3x
y = x2 cos 3x
Lineaarisen epähomogeenisen differentiaaliyhtälön
y' - 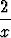 y = x2 cos 3x
y = x2 cos 3x
yleisen ratkaisun etsimiseksi on käsin laskettaessa ensin ratkaistava vastaava homogeeniyhtälö
y' - 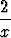 y = 0.
y = 0.
Tämä on separoituva: dy/y = 2dx/x. Homogeeniyhtälön yleinen ratkaisu on siten
y = Cx2.
Epähomogeenisen yhtälön yleiseen ratkaisuun tarvitaan lisäksi jokin epähomogeenisen yhtälön yksittäisratkaisu. Tämä voidaan etsiä joko arvaamalla sen muoto ja sijoittamalla sopiva yrite yhtälöön tai yleispätevällä vakion variointi -menettelyllä.
Yhtälön muodon perusteella tuntuisi järkevältä valita yritteeksi y = Ax2 sin 3x + Bx2 cos 3x ja pyrkiä määrittämään vakiot A ja B sopivasti. Tämän derivointi nimittäin tuottaa paitsi samanmuotoisia termejä myös muotoja x sin 3x ja x cos 3x olevia termejä, joita toisaalta syntyy myös kerrottaessa yrite y funktiolla 2/x.
Yritteen sijoittaminen yhtälöön antaa
2Ax sin 3x+3Ax2 cos 3x+2Bx cos 3x-3Bx2 sin 3x-2Ax sin 3x-2Bx cos 3x = x2 cos 3x
eli
3Ax2 cos 3x - 3Bx2 sin 3x = x2 cos 3x.
Jotta yhtälö olisi voimassa kaikilla arvoilla x, on ilmeisestikin oltava A = 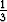 ja B = 0.
Yksittäisratkaisu on siis y =
ja B = 0.
Yksittäisratkaisu on siis y = 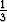 x2 sin 3x, jolloin epähomogeenisen yhtälön yleinen ratkaisu
on
x2 sin 3x, jolloin epähomogeenisen yhtälön yleinen ratkaisu
on
y = Cx2 + 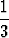 x2 sin 3x.
x2 sin 3x.
Epähomogeeniyhtälön yksittäisratkaisu voidaan myös hakea vakion varioinnilla, jolloin käytetään yritettä y = u(x)x2 ja pyritään määrittämään sopiva funktio u(x). Tekijä x2 on peräisin homogeeniyhtälön yleisestä ratkaisusta. Yritteen sijoittaminen yhtälöön antaa
x2u' + 2xu - 2xu = x2 cos 3x.
Tästä supistuu funktio u pois (näin käy aina) ja jäljelle jää vain derivaatan u'
sisältävä yhtälö u' = cos 3x. Tällä on ratkaisuna muiden ohella u =  sin 3x, jolloin
yksittäisratkaisuksi saadaan y = u(x)x2 =
sin 3x, jolloin
yksittäisratkaisuksi saadaan y = u(x)x2 = 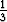 x2 sin 3x kuten edelläkin.
x2 sin 3x kuten edelläkin.