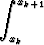 f(x, y(x)) dx.
f(x, y(x)) dx.
Kun differentiaaliyhtälö y' = f(x, y(x)) integroidaan puolittain välin [xk, xk+1] yli, saadaan
y(xk+1) - y(xk) = 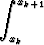 f(x, y(x)) dx.
f(x, y(x)) dx.
Adamsin – Bashforthin menetelmässä integroitava funktio f(x, y(x)) korvataan kolmannen asteen interpolaatiopolynomilla, jonka kuvaaja kulkee neljän viimeksi lasketun pisteen (xj , f(xj, yj)), j = k - 3, k - 2, k - 1, k, kautta. Muodostamalla polynomi ja integroimalla se saadaan integraalille approksimaatio
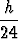 [55f(xk, yk) - 59f(xk-1, yk-1) + 37f(xk-2, yk-2) - 9f(xk-3, yk-3)].
[55f(xk, yk) - 59f(xk-1, yk-1) + 37f(xk-2, yk-2) - 9f(xk-3, yk-3)].
Menetelmän laskentakaava on siten
yk+1 = yk + 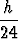 (55fk - 59fk-1 + 37fk-2 - 9fk-3),
(55fk - 59fk-1 + 37fk-2 - 9fk-3),
missä on merkitty lyhyesti fj = f(xj, yj). Kyseessä on moniaskelmenetelmä, koska uuden arvon laskeminen perustuu useaan aikaisempaan askeleeseen.
Jotta menetelmää voitaisiin käyttää, on tunnettava neljä aikaisempaa arvoa. Kaavaa ei siten voida käyttää alusta lähtien, vaan arvot y1, y2 ja y3 on laskettava jollakin muulla menetelmällä, tyypillisesti jollakin yksiaskelmenetelmällä kuten esimerkiksi Rungen – Kuttan menetelmällä.