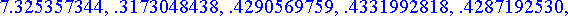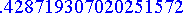Differentiaaliyhtälöryhmä

Ensimmäisen kertaluvun differentiaaliyhtälöryhmä — vaikkapa korkeamman kertaluvun yhtälöä vastaava normaaliryhmä — voidaan ratkaista numeerisesti täsmälleen samanlaisilla kaavoilla kuin ensimmäisen kertaluvun yhtälö y ' = f( x , y ). Edellytyksenä luonnollisesti on, että alkuehto on annettu.

Seuraavat koodit ovat täsmälleen samat kuin ensimmäisen kertaluvun yhtälöä koskevassa esimerkissä. (Solut on ajettava, jotta määritelmät tulevat voimaan.)

> restart;

> eulernum:=proc(f, x0, y0, h, xend)
local kend, x, y, i;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+h*f(x[i-1], y[i-1]);
od;
return [seq([x[k], y[k]], k=0..kend)];
end:

> pareuler:= proc(f, x0, y0, h, xend)
local kend, x, y, i;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+
h/2*(f(x[i-1],y[i-1])+
f(x[i],y[i-1]+h*f(x[i-1], y[i-1])));
od;
return [seq([x[k], y[k]], k=0..kend)];
end:

> rungekutta:= proc(f, x0, y0, h, xend)
local kend, x, y, i, k1, k2, k3, k4;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to kend do
x[i]:= x[i-1]+h;
k1:= h*f(x[i-1], y[i-1]);
k2:= h*f(x[i-1]+h/2, y[i-1]+k1/2);
k3:= h*f(x[i-1]+h/2, y[i-1]+k2/2);
k4:= h*f(x[i-1]+h, y[i-1]+k3);
y[i]:= y[i-1]+1/6*(k1+2*k2+2*k3+k4);
od;
return [seq([x[k], y[k]], k=0..kend)];
end:

> adamsbashforth:= proc(f, x0, y0, h, xend)
local kend, x, y, i, k1, k2, k3, k4;
kend:= round((xend-x0)/h);
x[0]:= x0;
y[0]:= y0;
for i from 1 to 3 do
x[i]:= x[i-1]+h;
k1:= h*f(x[i-1], y[i-1]);
k2:= h*f(x[i-1]+h/2, y[i-1]+k1/2);
k3:= h*f(x[i-1]+h/2, y[i-1]+k2/2);
k4:= h*f(x[i-1]+h, y[i-1]+k3);
y[i]:= y[i-1]+1/6*(k1+2*k2+2*k3+k4);
od;
for i from 4 to kend do
x[i]:= x[i-1]+h;
y[i]:= y[i-1]+h/24*(
55*f(x[i-1], y[i-1])-
59*f(x[i-2], y[i-2])+
37*f(x[i-3], y[i-3])-
9*f(x[i-4], y[i-4]))
od;
return [seq([x[k], y[k]], k=0..kend)];
end:

Esimerkkinä olkoon differentiaaliyhtälö x '' + xy = 0 alkuehtona y (0) = 0, y '(0) = 1 . Kyseessä on Airyn yhtälö, jossa x-akselin suunta on käännetty, ts. x :n merkki on vaihdettu. Yhtälöä vastaava normaaliryhmä muodostuu kahdesta yhtälöstä y ' = z , z ' = - xy alkuehtona y (0) = 0, z (0) = 1. Vektorimuodossa normaaliryhmä on Y ' = F( x , Y ); oikean puolen vektoriarvoinen funktio määritellään Maple lle seuraavasti:

> f:= unapply([Y[2], -x*Y[1]], x, Y);

Askelpituus ja arvo, jolla alkuehto annetaan:

> h:= 0.1;

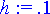
> x0:= 0;

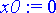
Tuntemattomana funktiona on vektori Y = ( y , z ), joten alkuarvo on myös vektori:

> y0:= [0,1];

Lasketaan välillä [0, 10]:

> xend:= 10;

Ratkaisufunktion approksimaatio jokaisessa pisteessä saadaan kaksikomponenttisena vektorina. Edellinen komponentti on itse funktion y arvo, jälkimmäinen sen derivaatan z = y ' arvo:

> eulerdata:= eulernum(f, x0, y0, h, xend):

Muuttujaan eulerdata talletettu tulostus on huomattavan pitkä.

Tästä voidaan poimia vain argumentin x ja funktion y arvot indeksoimalla, minkä jälkeen voidaan piirtää kuva:

> poiminta:= [seq([eulerdata[k][1], eulerdata[k][2][1]], k=1..xend/h+1)]:

> eulerkuva:= plot(poiminta, style=point):
eulerkuva;

Vastaavat laskut muita menetelmiä käyttäen:

> pareulerdata:= pareuler(f, x0, y0, h, xend):

> poiminta:= [seq([pareulerdata[k][1], pareulerdata[k][2][1]], k=1..xend/h+1)]:

> pareulerkuva:= plot(poiminta, style=point):
pareulerkuva;

> rungekuttadata:= rungekutta(f, x0, y0, h, xend):

> poiminta:=[seq([rungekuttadata[k][1], rungekuttadata[k][2][1]], k=1..xend/h+1)]:

> rungekuttakuva:= plot(poiminta, style=point):
rungekuttakuva;

> adamsbashforthdata:= adamsbashforth(f, x0, y0, h, xend):

> poiminta:= [seq([adamsbashforthdata[k][1], adamsbashforthdata[k][2][1]], k=1..xend/h+1)]:

> adamsbashforthkuva:= plot(poiminta, style=point):
adamsbashforthkuva;

Esimerkkinä oleva alkuarvoprobleema voidaan ratkaista myös tarkasti Airyn funktioiden avulla.

> dyht:= diff(y(x), x, x)+x*y(x)=0 ;

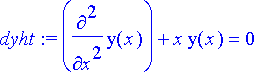
> tarkkaratkaisu:= dsolve({dyht, y(0)=0, D(y)(0)=1}, y(x));

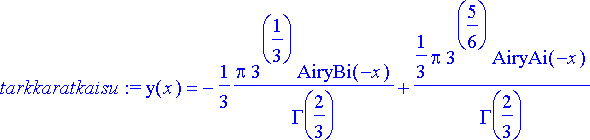
> tarkkakuva:= plot(rhs(tarkkaratkaisu), x=0..xend):
tarkkakuva;

Eri menetelmillä saadut approksimaatiot ja tarkka ratkaisu verrattuina:

> with(plots):

Warning, the name changecoords has been redefined

> display(eulerkuva, pareulerkuva, rungekuttakuva, adamsbashforthkuva, tarkkakuva);

Tarkan ratkaisun tarkkuus riippuu luonnollisesti siitä, miten Maple laskee ratkaisussa esiintyvien Airyn funktioiden ja gammafunktion arvot.

Vertailun vuoksi alkuarvoprobleema voidaan ratkaista myös Maple n käyttämällä numeerisen ratkaisemisen algoritmilla, joka edellä esitettyjä menetelmiä kehittyneempi:

> numeerinenratkaisu:= dsolve({dyht, y(0)=0, D(y)(0)=1}, y(x));

Tulos on ratkaisua approksimoiva proseduuri, jonka arvo välin päätepisteessä voidaan laskea tavalliseen tapaan. Eri ratkaisujen antamat arvot loppupisteessä :

> eulerdata[-1][2][1],
pareulerdata[-1][2][1],
rungekuttadata[-1][2][1],
adamsbashforthdata[-1][2][1],
evalf(subs(x=xend, rhs(tarkkaratkaisu))),
subs(numeerinenratkaisu(xend), y(x));