Alkuarvoprobleeman
y' = f(x, y), y(x0) = y0
ratkaisun ensimmäisen asteen Taylorin kehitelmä pisteessä xk on
| y(xk + h) | = y(xk) + hy'(xk) + O(h2) | ||
| = y(xk) + hf(xk, y(xk)) + O(h2). |
yk+1 = yk + hf(xk, yk).
Numeerinen ratkaiseminen tapahtuu valitsemalla sopiva askelpituus h ja soveltamalla iteraatiokaavaa ensimmäisen kerran indeksillä k = 0, jolloin oikealle puolelle sijoitetaan alkuehdossa olevat arvot ja saadaan lasketuksi y1. Tämä on approksimaatio ratkaisufunktion arvolle pisteessä x1 = x0 + h. Tämän jälkeen askel toistetaan arvolla k = 1 yleensä samaa askelpituutta h käyttäen, ja saadaan y2, joka approksimoi ratkaisufunktion arvoa pisteessä x2 = x1 + h, jne.
Koska f(xk , yk) = y'(xk) on ratkaisufunktion kulmakerroin pisteessä xk, Eulerin menetelmässä edetään pisteestä (xk, yk) ratkaisukäyrän tangentin suuntaan. Tästä aiheutuu luonnollisesti virhe, joka yleensä on sitä suurempi, mitä pitempää askelpituutta h käytetään. Differentiaaliyhtälön luonteesta riippuu, kumuloituvatko virheet useammassa askelessa vai eivät.
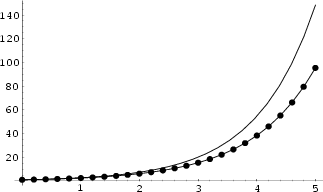
Oheiset kuvat esittävät alkuarvoprobleemojen y' = y, y(0) = 1 ja y' = -y, y(0) = 1 tarkkoja ratkaisuja ja niiden Eulerin menetelmän mukaisia approksimaatioita suhteellisen suurta askelpituutta h = 0.2 käytettäessä. Edellisessä tapauksessa virheet kumuloituvat, jälkimmäisessä alun kumuloitumisen jälkeen virhe katoaa.
Eulerin menetelmä voidaan johtaa myös integroimalla differentiaaliyhtälö välin [xk, xk+1] yli:
y(xk+1) - y(xk) =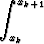 
f(x, y(x)) dx.
Kun integraalin approksimaatioksi otetaan välin pituuden h ja välin alkupisteessä lasketun funktion arvon f(xk, y(xk)) tulo, päädytään samaan iteraatiokaavaan kuin edellä.