 akxk
akxk
Olkoon tarkasteltavana toisen kertaluvun lineaarinen ja homogeeninen differentiaaliyhtälö y'' + xy = 0 (Airyn yhtälö, missä muuttujan x merkki on vaihdettu, ts. x-akselin suunta on käännetty).
Tämän sarjaratkaisu kehityskeskuksena origo saadaan yritteen
y =  akxk
akxk
avulla. Sijoittaminen yhtälöön antaa
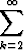 k(k - 1)akxk-2 +
k(k - 1)akxk-2 + 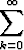 akxk+1 = 0
akxk+1 = 0
eli
2a2 +6a3 x+12a4x2+20a5x3+30a6x4+42a7x5+. . . +a0x+a1x2+a2x3+a3x4+a4x5+. . . = 0.
Koska oikea puoli on = 0, tulee myös vasemmalla olla jokaisen x:n potenssin kertoimen = 0, mikä johtaa yhtälöryhmään
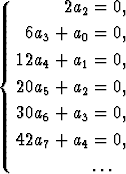
Yhtälöryhmän ratkaisussa voidaan ilmeisesti a0 ja a1 valita vapaasti ja välttämättä on a2 = 0. Kertoimesta a3 alkaen kukin kerroin lasketaan aina kolmanneksi edellisen kertoimen avulla, ts. kertoimet a5, a8, a11 jne. ovat = 0, kertoimet a3, a6, a9 jne. määräytyvät kertoimen a0 avulla ja vastaavasti kerroin a1 määrää kertoimet a4, a7, a10 jne.
Kuvatunkaltaiselle kertoimien rekursiiviselle laskemiselle voidaan myös johtaa yleinen kaava. Kun yhtälön
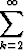 k(k - 1)akxk-2 +
k(k - 1)akxk-2 + 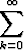 akxk+1 = 0
akxk+1 = 0
edellisessä summassa indeksit numeroidaan uudelleen merkitsemällä j = k - 2 ja jälkimmäisessä summassa merkitsemällä j = k + 1, saadaan
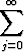 (j + 2)(j + 1)aj+2xj +
(j + 2)(j + 1)aj+2xj + 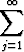 aj-1xj = 0
aj-1xj = 0
eli
2a2 + 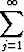 [(j + 2)(j + 1)aj+2 + aj-1]xj = 0.
[(j + 2)(j + 1)aj+2 + aj-1]xj = 0.
Koska kaikkien potenssien xj kertoimien pitää olla = 0, on siis oltava
a2 = 0, aj+2 = -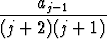 , j = 1, 2, 3, . . . .
, j = 1, 2, 3, . . . .
Ratkaisuun jää kaksi määräämätöntä vakiota, a0 ja a1. Nämä ovat toisen kertaluvun differentiaaliyhtälön yleisessä ratkaisussa esiintyvät kaksi integroimisvakiota. Kun muut kertoimet rekursiota käyttäen lasketaan näiden avulla, saadaan
| y = | a0 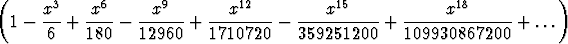 | ||
| + | a1 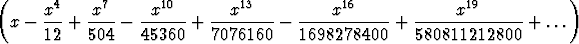 . . |
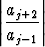 =
= 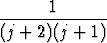
ja tämän raja-arvo on = 0, kun j 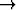
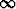 , sarjaratkaisu suppenee kaikilla muuttujan x
arvoilla potenssisarjojen teorian yleisten lauseiden mukaisesti. Tämä ei kuitenkaan
merkitse, että sarjoja voitaisiin käyttää ratkaisufunktioiden numeeristen arvojen
laskemiseen: argumentista x riippuen sarjojen suppeneminen saattaa olla hidasta ja
laskenta erittäin altista pyöristysvirheille.
, sarjaratkaisu suppenee kaikilla muuttujan x
arvoilla potenssisarjojen teorian yleisten lauseiden mukaisesti. Tämä ei kuitenkaan
merkitse, että sarjoja voitaisiin käyttää ratkaisufunktioiden numeeristen arvojen
laskemiseen: argumentista x riippuen sarjojen suppeneminen saattaa olla hidasta ja
laskenta erittäin altista pyöristysvirheille.