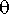Tavallinen heiluri

Otetaan tarkastelun kohteeksi tavallinen yksinkertainen heiluri. Tämä koostuu kitkattomaan niveleen kiinnitetystä (massattomasta) varresta sekä sen päässä olevasta kuulasta. Olkoon varren pituus L ja sen päässä olevan kuulan massa m . Kun heiluri poikkeutetaan tasapainoasemastaan ja se vapautetaan, syntyy heiluriliike. Rajoitutaan tarkastelemaan tasossa tapahtuvaa liikettä, jolloin heilurin asema voidaan ilmaista kulmalla 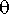, joka osoittaa poikkeaman pystysuorasta suunnasta.

Heilurin kuulaan vaikuttaa painovoima mg . Tämä voima yhdessä varren tukivoiman kanssa aiheuttavat tangentiaalisen voiman 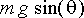heilurin ympyräkaaren muotoiselle liikeradalle. Newtonin toisen lain mukaisesti tämän voiman tasapainottaa heilurille aiheutuva kulmakiihtyvyys 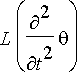jota vastaava voima on 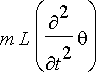. Nämä voimat siis kumoavat toisensa, eli saamme differentiaaliyhtälön

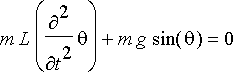
eli

( ).

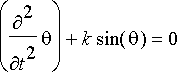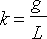Tämän differentiaaliyhtälön ratkaisu ei ole alkeisfunktio. Jos kulma 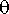on pieni, yhtälössä käytetään usein approksimaatiota 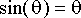, jolloin perusfunktiot tarjoavat approksimatiivisen ratkaisun muotoa

.

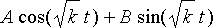Lasketaan tarkalle heiluriyhtälölle numeerinen ratkaisu ja tarkastellaan kulman 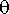aikariippuvuutta. Tämän jälkeen rakennetaan tarkkaan ratkaisuun perustuen animaatio heilurin liikkeelle.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.

> restart;

Heiluria kuvaava toisen kertaluvun differentiaaliyhtälö on helposti ilmaistavissa normaaliryhmänä.

> ryhma:= diff(theta(t), t)=omega(t), diff(omega(t), t)=-k*sin(theta(t));

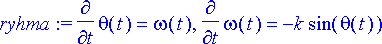
Ongelman tuntemattomat funktiot ovat heilurin kulma ja kulmanopeus.

> tuntemattomat:= {theta(t), omega(t)};

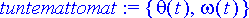
Olkoon k = 1. Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna yhden radiaanin kulmaan.

> k:= 1: alkuehto1:= theta(0)=1, omega(0)=0;

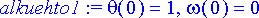
Ratkaistaan differentiaaliyhtälöryhmä numeerisesti.

> rtk:= dsolve({ryhma, alkuehto1}, tuntemattomat, numeric, output=listprocedure);

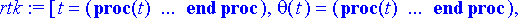
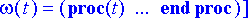
Poimitaan ratkaisusta kulma 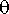ja kulmanopeus .

> kulmat:= subs(rtk, theta(t)), subs(rtk, omega(t)):

Piirretään kuvaaja, jossa näemme punaisella heilurin kulman 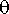, sekä vihreällä kulmanopeuden .

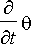> plot([kulmat], 0..15);

Heilurin kulma ajan funktiona muistuttaa kosinikäyrää. Tarkasteltu heilurin maksimiheilahduskulma on varsin suuri, jolloin aproksimaation 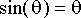tarjoama differentiaaliyhtälön ratkaisu (esitetyillä alkuehdoilla) 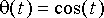on huonohko. Kuitenkin modifioimalla ratkaisun taajuutta sopivalla kertoimella, saadaan heilurin värähtelylle varsin hyvän alkeisfunktioapproksimaation.

Alla heilurin paikkaa (vihreä) approksimoidaan funktion 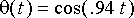punaisella pisteviivalla.

> with(plots):

Warning, the name changecoords has been redefined

> display(plot([t, cos(0.94*t), t=0..15], style=point), plot(kulmat[1], 0..15, color=green));

Seuraavaksi määritämme tarvittavat työkalut heilurin värähtelyn animoimiseksi. Värähtelevän heilurin lisäksi kuvassa näkyvät heilurin kuulaan vaikuttavat voimat. Varren tukivoima on punainen ja maan vetovoima sininen, vihreisiin osakomponentteihin jaettuna. Kyseessä on Maple lla kirjoitettu ohjelmakoodi.

> with(plottools):

> kuula:= proc(kulma, varsi)
local kuulax, kuulay;
kuulax:= varsi*sin(kulma);
kuulay:= -varsi*cos(kulma);
disk([kuulax, kuulay],
varsi/10,color=khaki);
end:

tanko:=proc(kulma, varsi)
line([0,0], [0.9*varsi*sin(kulma),
-0.9*varsi*cos(kulma)], thickness=3);
end:

nuolet:=proc(kulma,varsi)
display(
arrow([varsi*sin(kulma),
-varsi*cos(kulma)],
[varsi*sin(kulma),
-varsi*cos(kulma)-20],
0.1, 3, 0.2, color=blue),
arrow([varsi*sin(kulma),
-varsi*cos(kulma)],
[varsi*sin(kulma)
+20*cos(kulma)*sin(kulma),
-varsi*cos(kulma)
-20*cos(kulma)*cos(kulma)],
0.1, 3, 0.2, color=green),
arrow([varsi*sin(kulma),
-varsi*cos(kulma)],
[varsi*sin(kulma)
-20*sin(kulma)*cos(kulma),
-varsi*cos(kulma)
-20*sin(kulma)*sin(kulma)],
0.1, 3, 0.2, color=green),
arrow([varsi*sin(kulma),
-varsi*cos(kulma)],
[varsi*sin(kulma)
-20*sin(kulma)*cos(kulma),
-varsi*cos(kulma)
+20*cos(kulma)*cos(kulma)],
0.1, 3, 0.2, color=red));
end:

heiluri:= proc(kulma, aika)
local varsi, k;
varsi:= 50;
k:= kulma(aika*67/500);
display(
nuolet(k, varsi),
kuula(k, varsi),
tanko(k, varsi),
rectangle([-(varsi+10), 0],
[varsi+10, 5], color=gray),
axes=NONE, scaling=constrained);
end:

Animaatio on lista peräkkäisiä kuvia, jotka on ensin laskettava. Animaatio käynnistyy viemällä hiiren osoitin kuvan päälle ja valitsemalla hiiren oikealla napilla esiin tulevasta valikosta A n imation -> P l ay . Animaatiosta saa jatkuvan valitsemalla em. valikosta A n imation -> C ontinuous .

> display(seq(heiluri(kulmat[1], k), k=0..49), insequence=true, axes=NONE, scaling=CONSTRAINED);

Entä mitä heilurillemme tapahtuu, jos sille annetaan hieman vauhtia? Tarkastellaan ensin tilannetta, jossa alkuehtoon lisätään vauhtia -1.5 rad/s.

> alkuehto2:= theta(0)=1, omega(0)=-1.5;

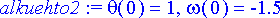
Numeerinen ratkaisu:

> rtk:= dsolve({ryhma, alkuehto2}, tuntemattomat, numeric, output=listprocedure);

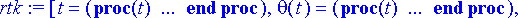
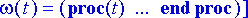
Piirretään jälleen kuvaaja, jossa punaisella on heilurin kulma 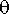sekä vihreällä kulmanopeus .

> kulmat:= subs(rtk, theta(t)), subs(rtk, omega(t)):

> plot([kulmat], 0..15);

Alkeisfunktioiden tarjoamat ratkaisut eivät enää tunnu enää kovinkaan sopivilta. Animoidaan jälleen heilurin liikettä, jotta nähdään, mitä tapahtuu

> display(seq(heiluri(kulmat[1], k), k=0..66), insequence=true, axes=NONE, scaling=CONSTRAINED);

Mitä heilurille tapahtuu kun vauhtia annetaan vielä enemmän? Kokeillaan alkuehtoa 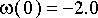rad/s ja lasketaan.

> alkuehto3:= theta(0)=1, omega(0)=-2;

> rtk:= dsolve({ryhma, alkuehto3}, tuntemattomat, numeric, output=listprocedure);

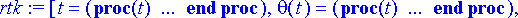
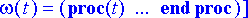
> kulmat:= subs(rtk, theta(t)), subs(rtk, omega(t));

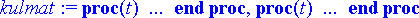
Ja animoimme vielä kerran.

> display(seq(heiluri(kulmat[1], k), k=0..30), insequence=true, axes=NONE, scaling=CONSTRAINED);

Tarkastellaan seuraavaksi heilurien liikeratoja faasitasossa. Olkoon x-akselina heilurin liikkeen kulma ja y-akselina sen kulmanopeus.

Käytämme piirtämiseen DEtools -paketin DEplot -komentoa. Samalla saamme kuvaan myös suuntakentän.

> with(DEtools):

Warning, the name translate has been redefined

> DEplot([ryhma], [theta(t),omega(t)], t=-7..7, theta=-Pi..3*Pi, omega=-4..4, [[alkuehto1], [alkuehto2], [alkuehto3]], stepsize=0.05);

Sisin suljettu käyrä kuvaa ensimmäistä heiluriliikettä, ulompi toista. Jatkuva värähtelykäyrä kuvaa kolmatta heiluriliikettä.

Tehtäviä

Heiluriliikkeet, jotka eivät tee kokonaisia pyörähdyksiä, muodostavat umpinaisen käyrän. Pyörivä heiluri muodostaa jatkuvan värähtelykäyrän. Mitä näillä faasitasokuvilla kuvataan?

Etsi heilurin alkuehtoja muokkaamalla heiluriliike, jossa heiluri juuri ja juuri pyörähtää ympäri. Mikä on lepoasennosta lähdettäessä tarvittava kulmanopeus? Miltä kyseinen liike näyttää faasitasossa?