Sovellukset : Heilurit
Kaksoisheiluri
Kaksoisheiluri koostuu kitkattomalla nivelellä kiinnitetystä heiluritangosta, jonka päässä on kuula, sekä toisesta heiluritangosta, joka on kiinnitetty kitkattomalla nivelellä edelliseen kuulaan. Myös toisen tangon päässä on kuula. Olkoot heilurien varsien pituudet =
L
ja niiden päissä olevien kuulien massat
![m[1]](Images/heiluri21.gif) ja
ja
![m[2]](Images/heiluri22.gif) . Kun heilurit poikkeutetaan tasapainoasemastaan siten, että varret ovat samassa pystysuorassa tasossa, ja systeemi vapautetaan, syntyy heilahdusliike. Systeemin asento voidaan ilmaista kahdella kulmalla: massan
. Kun heilurit poikkeutetaan tasapainoasemastaan siten, että varret ovat samassa pystysuorassa tasossa, ja systeemi vapautetaan, syntyy heilahdusliike. Systeemin asento voidaan ilmaista kahdella kulmalla: massan
![m[1]](Images/heiluri23.gif) varsi muodostaa kulman
varsi muodostaa kulman
![theta[1]](Images/heiluri24.gif) pystysuoran suunnan kanssa ja massan
pystysuoran suunnan kanssa ja massan
![m[2]](Images/heiluri25.gif) varsi vastaavalla tavalla kulman
varsi vastaavalla tavalla kulman
![theta[2]](Images/heiluri26.gif) .
.
![[Maple Bitmap]](Images/heiluri27.gif)
Systeemille voidaan johtaa seuraavat liikeyhtälöt. Johto on hieman hankala, mutta voidaan ehkä helpoimmin tehdä Lagrangen teorian avulla. (Ks. tätä käsittelevää Maple-dokumenttia.)
![diff(theta[1],`$`(t,2))+m*diff(theta[2],`$`(t,2))*c...](Images/heiluri28.gif)
![sin(theta[1]) = 0](Images/heiluri29.gif) ,
,
![diff(theta[2],`$`(t,2))+diff(theta[1],`$`(t,2))*cos...](Images/heiluri210.gif)
![sin(theta[2]) = 0](Images/heiluri211.gif) ,
,
missä
![m = m[2]/(m[1]+m[2])](Images/heiluri212.gif) .
.
Merkitään
k
=
g
/
L
.
Seuraavassa lasketaan heiluriyhtälöille numeeriset ratkaisut ja tarkastellaan heilahduskulmien aikariippuvuutta. Tämän jälkeen rakennetaan animaatio heilurin liikkeelle. Lopuksi tarkastellaan tilannetta faasitasossa.
Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat.
>
restart;
Heiluria kuvaava toisen kertaluvub differentiaaliyhtälöryhmä on ilmaistavissa normaaliryhmänä.
>
ryhma:= diff(theta[1](t), t)=omega[1](t), diff(omega[1](t), t)+m*diff(omega[2](t), t)*cos(theta[2](t)-theta[1](t))-m*diff(theta[2](t), t)^2*sin(theta[2](t)-theta[1](t))+k*sin(theta[1](t))=0, diff(theta[2](t), t)=omega[2](t), diff(omega[2](t), t)+diff(omega[1](t), t)*cos(theta[2](t)-theta[1](t))+diff(theta[1](t), t)^2*sin(theta[2](t)-theta[1](t))+k*sin(theta[2](t))=0;
,t) = omega[1](t), diff(om...](Images/heiluri213.gif)
,t) = omega[1](t), diff(om...](Images/heiluri214.gif)
,t) = omega[1](t), diff(om...](Images/heiluri215.gif)
,t) = omega[1](t), diff(om...](Images/heiluri216.gif)
Ongelman tuntemattomat funktiot ovat heilurin kahden eri osan kulmat ja niiden kulmanopeudet.
>
tuntemattomat:= {theta[1](t), omega[1](t), theta[2](t), omega[2](t)};
, omega[1](t), omega[2...](Images/heiluri217.gif)
Määritetään vakiot
k
= 1 ja
m =
0.5 (
![m[1] = m[2]](Images/heiluri218.gif) ) . Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna mallikuvan mukaisesti.
) . Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna mallikuvan mukaisesti.
>
k:= 1: m:= 0.5: alkuehto:= theta[1](0)=Pi/6, omega[1](0)=0, theta[2](0)=Pi/3, omega[2](0)=0;
 = 1/6*Pi, omega[1](0) = 0, ...](Images/heiluri219.gif)
Ratkaistaan differentiaaliyhtälöryhmä numeerisesti.
>
rtk:= dsolve({ryhma, alkuehto}, tuntemattomat, numeric, output=listprocedure);
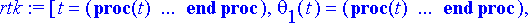
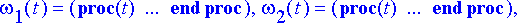
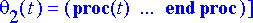
Poimitaan ratkaisusta kulmat
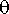 ja kulmanopeudet
ja kulmanopeudet
 .
.
>
kulmat:= subs(rtk, [theta[1](t), theta[2](t), omega[1](t), omega[2](t)]):
Piirretään kuvaajat sekä heilurien kulmille että kulmanopeuksille ajan suhteen. Kuulan
![m[1]](Images/heiluri225.gif) suureet on piirretty punaisella ja kuulan
suureet on piirretty punaisella ja kuulan
![m[2]](Images/heiluri226.gif) suureet vihreällä. Ensin kulmat.
suureet vihreällä. Ensin kulmat.
>
plot([kulmat[1], kulmat[2]], 0..100);
![[Maple Plot]](Images/heiluri227.gif)
Vaikka värähtelyt ovat varsin samankaltaisia, ne eivät kuitenkaan toista mitään selkeästi erottuvaa värähtelyä. Vastaavat kulmanopeuksien kuvaajat.
>
plot([kulmat[3], kulmat[4]], 0..100);
![[Maple Plot]](Images/heiluri228.gif)
Derivaatta käyttäytyy kuten kulmakin, eli värähtelyssä ei ole havaittavissa jaksoa. Tämä käyttäytyminen on tyypillistä kaoottiselle värähtelylle. Tarkastellaan animaation avulla, miltä kyseinen värähtely näyttää.
Seuraavaksi määritämme tarvittavat työkalut heilurin värähtelyn animoimiseksi. Kyseessä on
Maple
lla kirjoitettu ohjelmakoodi.
>
with(plots): with(plottools):
Warning, the name changecoords has been redefined
>
kuula:= proc(x, y, kulma, varsi)
local kuulax, kuulay;
kuulax:= x+varsi*sin(kulma);
kuulay:= y-varsi*cos(kulma);
disk([kuulax,kuulay], varsi/10,
color=khaki);
end:
tanko:=proc(x,y,kulma,varsi)
line([x,y], [x+0.9*varsi*sin(kulma),
y-0.9*varsi*cos(kulma)], thickness=3);
end:
kaksoisheiluri:= proc(kulma, aika)
local varsi, k1, k2;
varsi:= 50;
k1:= kulma[1](aika*1/3);
k2:= kulma[2](aika*1/3);
display(
kuula(0, 0, k1, varsi),
kuula(varsi*sin(k1), -varsi*cos(k1),
k2, varsi),
tanko(0, 0, k1, varsi),
tanko(varsi*sin(k1)+0.1*varsi*sin(k2),
-varsi*cos(k1)-0.1*varsi*cos(k2),
k2, 0.9*varsi),
rectangle([-(varsi+10),0],
[varsi+10,5], color=gray),
axes=NONE, scaling=constrained);
end:
Animaatio on lista peräkkäisiä kuvia, jotka on ensin laskettava. Animaatio käynnistyy viemällä hiiren osoitin kuvan päälle ja valitsemalla hiiren oikealla napilla esiin tulevasta valikosta
A
n
imation
->
P
l
ay
. Animaatiosta saa jatkuvan valitsemalla em. valikosta
A
n
imation
->
C
ontinuous
.
>
display(seq(kaksoisheiluri([kulmat[1], kulmat[2]], k), k=0..99), insequence=true, axes=NONE, scaling=CONSTRAINED);

Tarkastellaan seuraavaksi heilurien liikeratoja faasitasossa. Olkoon x-akselina heilurin liikkeen kulma ja y-akselina sen kulmanopeus. Ensimmäisen heilurin liike on piirretty vihreällä ja toisen sinisellä.
Heiluriliikkeiden kuvaajat faasitasossa piirretään
DEtools
-paketin
DEplot
-komennolla ja yhdistetään samaan kuvaan
display
-komennolla.
>
with(DEtools):
Warning, the name translate has been redefined
>
kuva1:= DEplot([ryhma], [theta[1](t), theta[2](t), omega[1](t), omega[2](t)], t=0..100, theta[1]=-1.2..1.2, omega[1]=-1.2..1.2, [[alkuehto]], scene=[theta[1],omega[1]], stepsize=0.05, linecolor=green, thickness=1):
kuva2:= DEplot([ryhma], [theta[1](t), theta[2](t), omega[1](t), omega[2](t)], t=0..100, theta[2]=-1.2..1.2, omega[2]=-1.2..1.2, [[alkuehto]], scene=[theta[2], omega[2]], stepsize=0.05, linecolor=blue, thickness=1):
display(kuva1, kuva2, scaling=constrained, axes=normal, labels=["",""]);
![[Maple Plot]](Images/heiluri230.gif)
Vertaamalla saatua tulosta tavallisen heilurin vastaavaan faasitasokuvaan, käy selväksi, mikä olennainen ero kaoottisen ja tavallisen heilurin välillä on. Tasaisesti toistuvan värähtelykierron sijaan kaoottinen heiluri määrittää tietyn alueen faasitasossa, jonka sisällä heilurin rata kiertää.
Tehtäviä
Kaoottisen ilmiön yksi tunnuspiirre on se, että pieni muutos alkutilanteessa aiheuttaa helposti suuren muutoksen lopputulokseen. Tarkastele tämän väitteen pätevyyttä muuttamalla hieman heilurin alkuehtoja, esimerkiksi 10%, ja vertaamalla saamaasi värähtelyä yllä esitettyihin kulma- ja kulmanopeuskuvaajiin rajoitetulla aikavälillä kaukana alkutilanteesta, esimerkiksi
t
= 90...100 s.
Muokataan heilurin alkuehtoja asettamalla
![theta[2] = Pi](Images/heiluri231.gif) hetkellä
t
= 0 s. Animoi saamasi heiluriliike. Animaatiokuvat vievät runsaasti koneen muistia, joten voit muistin vapauttamiseksi poistaa edellisen animaatiokuvasarjan ennen uuden laskemista. Tämä tapahtuu klikkaamalla kuva aktiiviseksi ja painamalla
delete
. Miltä kyseinen liike näyttää faasitasossa? Osaatko selittää mistä on kysymys? Entä miten nyt vaikuttaa yllä esitetty pieni alkuehdon muutos?
hetkellä
t
= 0 s. Animoi saamasi heiluriliike. Animaatiokuvat vievät runsaasti koneen muistia, joten voit muistin vapauttamiseksi poistaa edellisen animaatiokuvasarjan ennen uuden laskemista. Tämä tapahtuu klikkaamalla kuva aktiiviseksi ja painamalla
delete
. Miltä kyseinen liike näyttää faasitasossa? Osaatko selittää mistä on kysymys? Entä miten nyt vaikuttaa yllä esitetty pieni alkuehdon muutos?
Annetussa tehtävässä massat
![m[1]](Images/heiluri232.gif) ja
ja
![m[2]](Images/heiluri233.gif) on määritelty yhtä suuriksi (
k
= 1/2). Kokeile miten massan muuttaminen vaikuttaa heilurin käytökseen. Kumman, ylemmän vai alemman massan kaksinkertaistaminen aiheuttaa stabiilimman värähtelyn? Käytä päättelyn apuna faasitasokuvia. Miten saamasi tulos suhtautuu heilurille alkuehdossa annettuun energiaan?
on määritelty yhtä suuriksi (
k
= 1/2). Kokeile miten massan muuttaminen vaikuttaa heilurin käytökseen. Kumman, ylemmän vai alemman massan kaksinkertaistaminen aiheuttaa stabiilimman värähtelyn? Käytä päättelyn apuna faasitasokuvia. Miten saamasi tulos suhtautuu heilurille alkuehdossa annettuun energiaan?
Sovelluksia: tavallinen heiluri
Sovelluksia: kaksoisheilurin liikeyhtälöiden johto
Teoria: normaaliryhmä
Teoria: faasitaso
JP & SKK & MS 12.07.2001
![m[1]](Images/heiluri21.gif) ja
ja
![m[2]](Images/heiluri22.gif) . Kun heilurit poikkeutetaan tasapainoasemastaan siten, että varret ovat samassa pystysuorassa tasossa, ja systeemi vapautetaan, syntyy heilahdusliike. Systeemin asento voidaan ilmaista kahdella kulmalla: massan
. Kun heilurit poikkeutetaan tasapainoasemastaan siten, että varret ovat samassa pystysuorassa tasossa, ja systeemi vapautetaan, syntyy heilahdusliike. Systeemin asento voidaan ilmaista kahdella kulmalla: massan
![m[1]](Images/heiluri23.gif) varsi muodostaa kulman
varsi muodostaa kulman
![theta[1]](Images/heiluri24.gif) pystysuoran suunnan kanssa ja massan
pystysuoran suunnan kanssa ja massan
![m[2]](Images/heiluri25.gif) varsi vastaavalla tavalla kulman
varsi vastaavalla tavalla kulman
![theta[2]](Images/heiluri26.gif) .
.
![[Maple Bitmap]](Images/heiluri27.gif)
![diff(theta[1],`$`(t,2))+m*diff(theta[2],`$`(t,2))*c...](Images/heiluri28.gif)
![sin(theta[1]) = 0](Images/heiluri29.gif) ,
,
![diff(theta[2],`$`(t,2))+diff(theta[1],`$`(t,2))*cos...](Images/heiluri210.gif)
![sin(theta[2]) = 0](Images/heiluri211.gif) ,
,
![m = m[2]/(m[1]+m[2])](Images/heiluri212.gif) .
.
,t) = omega[1](t), diff(om...](Images/heiluri213.gif)
,t) = omega[1](t), diff(om...](Images/heiluri214.gif)
,t) = omega[1](t), diff(om...](Images/heiluri215.gif)
,t) = omega[1](t), diff(om...](Images/heiluri216.gif)
, omega[1](t), omega[2...](Images/heiluri217.gif)
![m[1] = m[2]](Images/heiluri218.gif) ) . Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna mallikuvan mukaisesti.
) . Alkuehdon määrittää tilanne, jossa heiluri on levossa poikkeutettuna mallikuvan mukaisesti.
 = 1/6*Pi, omega[1](0) = 0, ...](Images/heiluri219.gif)
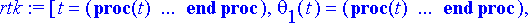
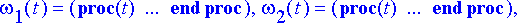
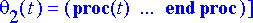
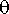 ja kulmanopeudet
ja kulmanopeudet
 .
.
![m[1]](Images/heiluri225.gif) suureet on piirretty punaisella ja kuulan
suureet on piirretty punaisella ja kuulan
![m[2]](Images/heiluri226.gif) suureet vihreällä. Ensin kulmat.
suureet vihreällä. Ensin kulmat.
![[Maple Plot]](Images/heiluri227.gif)
![[Maple Plot]](Images/heiluri228.gif)

![[Maple Plot]](Images/heiluri230.gif)
![theta[2] = Pi](Images/heiluri231.gif) hetkellä
t
= 0 s. Animoi saamasi heiluriliike. Animaatiokuvat vievät runsaasti koneen muistia, joten voit muistin vapauttamiseksi poistaa edellisen animaatiokuvasarjan ennen uuden laskemista. Tämä tapahtuu klikkaamalla kuva aktiiviseksi ja painamalla
delete
. Miltä kyseinen liike näyttää faasitasossa? Osaatko selittää mistä on kysymys? Entä miten nyt vaikuttaa yllä esitetty pieni alkuehdon muutos?
hetkellä
t
= 0 s. Animoi saamasi heiluriliike. Animaatiokuvat vievät runsaasti koneen muistia, joten voit muistin vapauttamiseksi poistaa edellisen animaatiokuvasarjan ennen uuden laskemista. Tämä tapahtuu klikkaamalla kuva aktiiviseksi ja painamalla
delete
. Miltä kyseinen liike näyttää faasitasossa? Osaatko selittää mistä on kysymys? Entä miten nyt vaikuttaa yllä esitetty pieni alkuehdon muutos? ![m[1]](Images/heiluri232.gif) ja
ja
![m[2]](Images/heiluri233.gif) on määritelty yhtä suuriksi (
k
= 1/2). Kokeile miten massan muuttaminen vaikuttaa heilurin käytökseen. Kumman, ylemmän vai alemman massan kaksinkertaistaminen aiheuttaa stabiilimman värähtelyn? Käytä päättelyn apuna faasitasokuvia. Miten saamasi tulos suhtautuu heilurille alkuehdossa annettuun energiaan?
on määritelty yhtä suuriksi (
k
= 1/2). Kokeile miten massan muuttaminen vaikuttaa heilurin käytökseen. Kumman, ylemmän vai alemman massan kaksinkertaistaminen aiheuttaa stabiilimman värähtelyn? Käytä päättelyn apuna faasitasokuvia. Miten saamasi tulos suhtautuu heilurille alkuehdossa annettuun energiaan?