Yksinkertainen vaihtovirtapiiri

Tarkastellaan piiriä, jossa on kela kytkettynä virtalähteeseen. Olkoon piirissä L henryn induktanssi.

Piiriin syötetty jännite kokee kelan aiheuttaman induktiivisen vastuksen, joka on muotoa

.

Mikäli piiriin syötetty jännite on sinimuotoista vaihtovirtaa , tulee sen olla samansuuruinen piirissä tapahtuvan jännitepudotuksen kanssa. on vaihtojännitteen kulmataajuus. Kirchhoffin lain mukaan voidaan piirille muodostaa yhtälö

,

missä on piiriin syötetyn jännitteen maksimiamplitudi ja I ( t ) piirissä kulkeva virta.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:

> restart;

Piirin virtaa kuvaava yhtälö.

> yhtalo:= L*diff(i(t), t)=E[0]*sin(omega*t);

Tarkastellaan tilannetta, jossa piiri on alussa vailla virtaa.

> alkuehto:= i(0)=0;

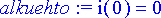
Ratkaistaan differentiaaliyhtälö piirissä kulkevan virran määrittämiseksi.

> rtk:= dsolve({yhtalo, alkuehto}, i(t));

Sijoitetaan muuttujat ja sievennetään ratkaisu.

> sij:= {L=0.1, E[0]=230, omega=2*Pi*50}:
jannite:= subs(sij, E[0]*sin(omega*t));
virta:= simplify(subs(sij, rhs(rtk)));

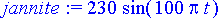
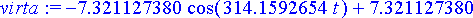
Piirretään kuvaaja virralle (punainen) ja piiriin syötetylle jännitteelle (E( t )/10, vihreä) ajan funktioina.

> plot([virta, jannite/10], t=0..0.1);

Piiriin syntyy jaksottainen virta. Käämi vastustaa piirissä virran muutosta, ja siten virta laahaa jännitevaihtelun perässä. Alkuehto määrää, minkä arvojen väliin virran värähtely asettuu.

Tehtävä

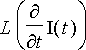Muokkaa virtapiirin differentiaaliyhtälöä siten, että ideaalin käämin sijaan piirissä on reaalinen käämi jolla on vastus R = 5 . Induktiivisen vastuksen aiheuttaman jännitepudotuksen lisäksi piirissä on jännitepudotus R I ( t ). Piirrä kuvaaja piirissä kulkevalle virralle ja syötetylle jännitteelle aikavälillä 0 - 0.1 s. Selitä havaitsemasi ilmiö.