![[Maple Bitmap]](Images/virtap31.gif)
| virtap3.mws |
Tässä esimerkissä tarkastellaan tavallista RLC-vaihtovirtapiiriä. Piirissä on kolme komponenttia, R ohmin vastus, L henryn induktanssi ja C faradin kapasitanssi.
![[Maple Bitmap]](Images/virtap31.gif)
Piiriin syötettyyn jännitteeseen kohdistuu kolme eri pudotusta,
![E[L] = L*diff(I(t),t)](Images/virtap32.gif) käämin yli,
käämin yli,
![E[R] = R*I(t)](Images/virtap33.gif) vastuksen yli sekä
vastuksen yli sekä
![E[C] = 1/C](Images/virtap34.gif)
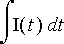 kondensaattorin yli.
kondensaattorin yli.
Näiden summasta syntyy piirin Kirchhoffin lain mukainen sähkömotorinen voima
E
(
t
). Mikäli piiriin syötetty jännite on sinimuotoista vaihtovirtaa E(
t
) =
![E[0]*sin(omega*t)](Images/virtap36.gif) , saadaan piirille yhtälö
, saadaan piirille yhtälö
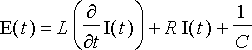
![int(I(t),t) = E[0]*sin(omega*t)](Images/virtap38.gif) ,
,
Integraalitermistä päästään eroon derivoimalla yhtälö ajan suhteen:
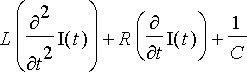
![I(t) = E[0]*omega*cos(omega*t)](Images/virtap310.gif) .
.
Tämä on differentiaaliyhtälö pakotetulle värähtelylle, jossa ulkoinen pakottava jännite on sinimuotoinen amplitudina
![E[0]](Images/virtap311.gif) .
.
Syötetään piirin yhtälö alkuehtoineen. Aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:
> restart;
Differentiaaliyhtälö:
> yhtalo:= L*diff(i(t), t$2)+R*diff(i(t), t)+i(t)/C=E[0]*omega*cos(omega*t);
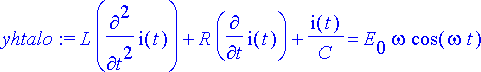
Ongelman tuntematon:
> tuntematon:= i(t);
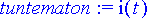
Tarkastellaan tilannetta, missä piirissä ei kulje tarkastelun alkuhetkellä virtaa. Annetaan tätä vastaava alkuehto:
> alkuehto:= i(0)=0, D(i)(0)=0;
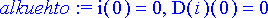
Piiri on vaimentamaoton, jos sen vastus on
R
= 0. Asetetaan yhtälöön tämänmukaiset alkuarvot; olkoon
L
= 0.1 H,
C
= 1
 F,
F,
![E[0]](Images/virtap316.gif) = 230 V,
= 230 V,
 = 50 × 2
= 50 × 2
 1/s.
1/s.
> yhtalo1:= subs({L=0.1, R=0, C=0.001, E[0]=230, omega=50*2*Pi}, yhtalo);
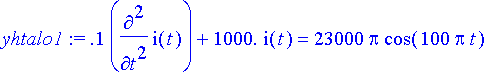
Ratkaistaan yhtälöryhmä.
>
dsolve({yhtalo1, alkuehto}, tuntematon):
virta1:= subs(%, i(t)):
simplify(%);
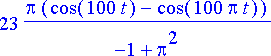
Virta näyttää muodostuvan kahden eritaajuisen kosinimuotoisen termin summasta. Toinen näistä aiheutuu piirin sisäisistä värähtelyominaisuuksista, toinen piiriin syötetystä ulkoisesta jännitteestä. Piirissä syntyvän virran kuvaaja:
> plot(virta1, t=0..0.3);
![[Maple Plot]](Images/virtap321.gif)
Virta ei vaimene. Tämä värähtely on siis vaimentamattoman piirin vaste syöttöjännitteelle.
Seuraavaksi lasketaan piirin käyttäytyminen silloin, kun siinä on 3
 vastus.
vastus.
> yhtalo2:= subs({L=0.1, R=3, C=0.001, E[0]=230, omega=50*2*Pi}, yhtalo);
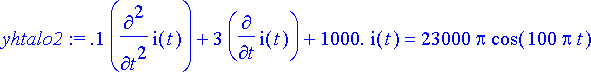
Ratkaistaan yhtälöryhmä.
>
dsolve({yhtalo2, alkuehto}, tuntematon):
virta2:= subs(%, i(t)):
simplify(%);
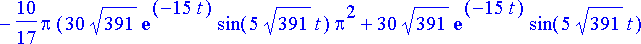
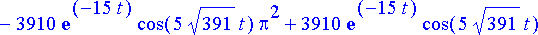
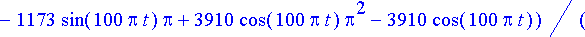
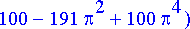
Ratkaisussa on jälleen kahden eri taajuuden termejä: Piirin sisäisistä ominaisuuksista johtuvien termien edessä on eksponentiaalinen vaimennuskerroin. Tämän takia kyseinen taajuus vähitellen kuolee pois. Virran kuvaaja:
> plot(virta2, t=0..0.3);
![[Maple Plot]](Images/virtap328.gif)
Kuva osoittaa, että vaikka vastus jatkuvasti kuluttaakin virtatehoa hukkaan lämpönä, virtalähde syöttää piiriin energiaa, joka ylläpitää värähtelyä.
Muuta tehtävän alkuehtoa sekä vaimentamattomassa että vaimennetussa tapauksessa. Miten tämä vaikuttaa piirin värähtelyyn?
Vaihdetaan piiriin käämi, jonka induktanssi on vain yksi kymmenesosa aikaisemmasta, 0.01 H. Tarkastele piirin käytöstä uudella käämillä, vastuksen kanssa ja ilman. Käytä kuvissa aiempaa pidempää aikaväliä. Vertaa saamiasi tuloksia aikaisempiin tuloksiin. Miten selität piirin käytöksen?