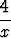 y' +
y' + 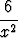 y = 0,
y = 0,
Lineaariset differentiaaliyhtälöt ovat varsin hyvin käyttäytyviä: alkuarvoprobleemalle on olemassa yksikäsitteinen ratkaisu sangen yleisillä edellytyksillä.
Lause. Olkoon tarkasteltavana normaalimuotoinen kertalukua n oleva lineaarinen (homogeeninen tai epähomogeeninen) differentiaaliyhtälö
y(n) + Pn-1(x)y(n-1) + . . . + P1(x)y' + P0(x)y = R(x)
(missä siis korkeimman kertaluvun derivaatan kerroin on = 1) ja alkuehto
y(x0) = y0, y'(x0) = y1, . . . , yn-1(x0) = yn-1.
Jos funktiot Pk, k = 0, 1, . . . , n - 1, ja R ovat jatkuvia tarkasteluvälillä [a, b], johon alkuehtokohta x0 kuuluu, niin alkuarvoprobleemalla on tällä välillä yksikäsitteinen ratkaisu.
Ehto yhtälön normaalimuotoisuudesta on oleellinen. Esimerkiksi Eulerin yhtälön x2 y'' - 4xy' + 6y = 0 kerroinfunktiot P2(x) = x2, P1(x) = -4x ja P0(x) = 6 ovat kyllä jatkuvia, mutta yhtälön yleinen ratkaisu y = C1x2 + C2x3 toteuttaa vakioista C1 ja C2 riippumatta alkuehdon y(0) = y'(0) = 0. Alkuarvoprobleemalla on tällöin äärettömän monta ratkaisua. Jos toisaalta alkuehtona on vaikkapa y(0) = 0, y'(0) = 1, ei ratkaisua löydy lainkaan. Normaalimuodossa yhtälö onkin
y'' - 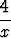 y' +
y' + 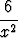 y = 0,
y = 0,
jolloin kerroinfunktiot eivät ole edes määriteltyjä alkuehtokohdassa x = 0.
Lause voidaan todistaa samaan tapaan kuin yleisen tapauksen ratkaisun olemassaoloa
koskeva lause. Oleellisena erona on, että suorakulmion sijasta voidaan tarkastella
y-suunnassa rajoittamatonta vyötä {(x, y) | a < x < b, -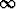 < y <
< y < 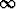 }. Seurauksena on,
että ei jouduta rajoittamaan väliä, jolla ratkaisu on olemassa.
}. Seurauksena on,
että ei jouduta rajoittamaan väliä, jolla ratkaisu on olemassa.