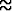Numeerinen näkökulma

Paitsi algebrallisesti differentiaaliyhtälö voidaan pyrkiä ratkaisemaan numeerisesti. Tällöin täytyy yhtälön lisäksi olla annettuna sellainen alkuehto, että ratkaisu on yksikäsitteinen. Ratkaistavana on siten alkuarvoprobleema.

Ajatuksena on laskea diskreettejä argumentin arvoja vastaavat ratkaisufunktion arvot:

Jos alkuehto on annettu pisteessä x₀, niin muodostetaan pisteistö x₀ < x₁ < x₂ < . . . . Usein tämä on tasavälinen, ts. x_k+1 = x_k + h kaikilla k = 0, 1, 2, . . . . Tavoitteena on laskea ratkaisufunktion y approksimaatiot näissä pisteissä: y_k 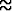y(x_k). (Pisteistö voi luonnollisesti sijaita myös alkuehtokohdasta taaksepäin: x₀ > x₁ > x₂ > . . . , jolloin h < 0.)

Approksimaatiot y_k lasketaan iteratiivisesti: arvon y_k+1 laskeminen perustuu jo aiemmin laskettuihin arvoihin y₀, y₁, . . . , y_k. Laskentamenetelmiä on useita erilaisia. Tyypillisesti ne ovat tietokonemenetelmiä.

Menetelmät ovat likimääräisiä ja tuottavat aina jossain määrin virheellisiä arvoja. Numeerinen laskenta tietokoneessa aiheuttaa myös aina pyöristysvirheitä. Laskennan tarkkuuden arviointi on siten oleellinen kysymys.

Eri menetelmät eroavat toisistaan tarvittavan laskentatyön suhteen ja sen suhteen, minkä tyyppisille differentiaaliyhtälöille ne soveltuvat. Argumenttiarvojen x_k etäisyys toisistaan, ts. askelväli h voi myös vaihdella, ja sen sopivalla valinnalla voidaan vaikuttaa laskennan tarkkuuteen. Tällöin puhutaan adaptiivisista menetelmistä.

Askelpituus h on yleensä melko pieni. Sen pienentäminen merkitsee ratkaisufunktion arvojen laskemista tiheämmin, mutta samalla laskentatyö kasvaa, koska halutulle tarkasteluvälille mahtuu useampia pisteitä x_k. Laskentatyön kasvaminen merkitsee usein myös laskennassa tapahtuvien pyöristysvirheiden kumuloitumista. Askelpituuden pienentäminen ei siten välttämättä johda tarkempaan ratkaisuun.

Tarvittavan laskentatyön määrä voi olla oleellinen: laskutoimitusten määrä jossakin sovellusongelmassa voi nousta niin suureksi, että sillä on oleellinen vaikutus laskenta-aikaan myös nopeita tietokoneita käytettäessä.