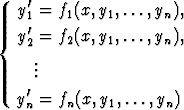
Toista tai korkeampaa kertalukua olevan differentiaaliyhtälöryhmän numeerinen ratkaiseminen perustuu vastaavan normaaliryhmän tarkasteluun. Tällöin on oleellista, että kyseessä on normaalimuotoinen ensimmäisen kertaluvun differentiaaliyhtälöryhmä alkuehtoineen, ei se, että kyseessä on korkeamman kertaluvun yhtälöstä syntynyt normaaliryhmä.
Olkoon tarkastelun kohteena siis normaalimuotoinen ryhmä
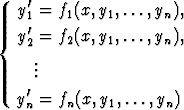
alkuehtona y1(x0) = y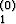
, y2(x0) = y
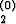, . . . , yn(x0) = y
.
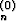Vektorimuodossa tämä on
Y ' = F (x, Y ), Y (x0) = Y (0),
missä
Y =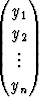 
, Y (0) = 
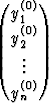, F (x, Y ) = 
.
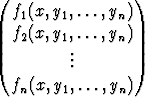Funktioille yj voidaan muodostaa Taylorin kehitelmät samalla tavoin kuin ensimmäisen kertaluvun yhtälöä tarkasteltaessa: derivaattojen laskemiseksi ryhmän jokaista yhtälöä on derivoitava muuttujan x suhteen. Approksimoitaessa lausekkeita saadaan jokaiselle funktiolle yj erikseen muotoa
y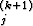
= y
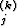+ gj(xk, Y (0), Y (1), . . . , Y (k), h)
oleva kaava funktionarvon yj(xk+1) approksimaation y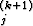
laskemiseen. (Huomaa:
Suluissa oleva yläindeksi (k) viittaa pisteessä xk laskettuun approksimaatioon. Kyseessä ei
ole derivaatan kertaluku.)
Kaavat voidaan yhdistää vektorimuotoon:
Y (k+1) = Y (k) + G(xk, Y (0), Y (1), . . . , Y (k), h).
Vektorimuotoinen yhtälö Y ' = F (x, Y ) voidaan myös integroida puolittain integroimalla jokainen komponenttiyhtälö erikseen. Täsmälleen samalla tavalla kuin yhden yhtälön tapauksessa tämä johtaa laskentakaavaan
Y (k+1) = Y (k) + I(xk, Y (0), Y (1), . . . , Y (k), h).
Ainoana erona on, että funktio I on vektoriarvoinen funktio.