1 Differentiaaliyhtälö
1.1 Peruskäsitteet
Tehtävä 1
Määrää seuraavien differentiaaliyhtälöiden laatu (tavallinen vai osittainen, normaalimuotoinen vai ei, kertaluku).| a) xy'' + 2y sin x = ex, | |||
| b) y' + sin(x + y) = sin x, | |||
| c) y'(y(x)) = y(x), | |||
d)  =  . |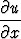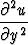
Tehtävä 2
Näytä, että y = 2x + Cex on differentiaaliyhtälön y' = y + 2(1 - x) yleinen ratkaisu. Määritä ratkaisukäyrä, joka kulkee pisteen a) (0, 1), b) (0, -1) kautta. Piirrä käyrät.Tehtävä 3
Osoita, että y = e-2x(C1 sin x + C2 cos x) on differentiaaliyhtälön y'' + 4y' + 5y = 0 ratkaisu. Määritä alkuehdon y(0) = y'(0) = 1 toteuttava ratkaisu.Tehtävä 4
Osoita, että y =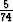
sin x + 
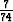cos x + C1ex + C2e6x on differentiaaliyhtälön
y'' - 7y' + 6y = sin x ratkaisu.
Tehtävä 5
Osoita, että y = C1ex + C2e2x + x on differentiaaliyhtälön y'' - 3y' + 2y = 2x - 3 ratkaisu.Tehtävä 6
Osoita, että differentiaaliyhtälöllä y'2 = 4y on ratkaisuna y = (x + C)2 ja y = 0; tässä C on vakio. Millaisia ovat ratkaisukäyrien kuvaajat? Mitä muita ratkaisuja differentiaaliyhtälöllä on?Tehtävä 7
Näytä, että funktiopari y = C1 cos x + C2 sin x, z = (C1 + C2) cos x + (C2 - C1) sin x toteuttaa differentiaaliyhtälöryhmän
.
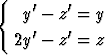Tehtävä 8
Olkoon f :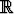
2 
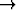
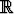differentioituva funktio ja olkoon y differentiaaliyhtälön
y' = f(x, y) alkuehdon y(x0) = y0 toteuttava ratkaisu. Johda lauseke derivaatalle y''(x0).
Tehtävä 9
Määritä alkuarvoprobleeman xy' = x + y, y(1) = 1 ratkaisukäyrän kaarevuus alkuehtopisteessä.Tehtävä 10
Yhtälöllä y' = y on ratkaisuna y = ex. Osoita, että sen jokainen muu ratkaisu poikkeaa tästä vain kerrannaisella vakiolla tarkastelemalla muotoa y = u(x)ex olevaa ratkaisua.Tehtävä 11
Olkoon f jatkuva kahden muuttujan funktio. Näytä, että yhtälön y' = yf(x, y) ratkaisukäyrät joko sivuavat x-akselia tai eivät kosketa sitä lainkaan.Tehtävä 12
Olkoot funktion f toisen kertaluvun osittaisderivaatat olemassa. Laske alkuarvoprobleeman y' = f(x, y), y(x0) = y0 ratkaisun y(x) kolmannen asteen Taylorin polynomi kehityskeskuksena x0.Tehtävä 13
Laske alkuarvoprobleeman yy'' + y' + y = 0, y(0) = 1, y'(0) = 0 ratkaisun neljännen asteen Maclaurinin polynomi. Sijoita tulos differentiaaliyhtälöön.Tehtävä 14
Laske alkuarvoprobleeman y'' = yy' - x2, y(0) = y'(0) = 1 ratkaisun neljännen asteen Maclaurinin polynomi. Sijoita tulos differentiaaliyhtälöön.Tehtävä 15
Tutki seuraavien differentiaaliyhtälöiden tai alkuarvoprobleemoiden ratkaisemista jonkin symbolisen tietokoneohjelman avulla:| a) y' = xy, b) y' = xy, y(1) = 2, c) y' = x2 - y2, y(0) = 1, | |||
| d) y'' - 4y' + 13y = x4, e) yy'' = y'2 + yy', y(0) = 2, y'(0) = 1, f) y'' + xy = 0. |
Tehtävä 16
Kirjoita differentiaaliyhtälö3x2 + 6xy2 + (6x2y + 4y3)y' = 0
muotoon y' = f(x, y). Tutki yhtälön ratkaisukäyriä numeerisesti.
1.2 Ratkaisukäyräparvet
Tehtävä 17
Muodosta suoraparven y = Cx + 2C2 (C parametri) differentiaaliyhtälö. Yhtälöllä on erikoisratkaisuna eräs toisen asteen polynomi; määritä tämä. Piirrä muutamien yksityisratkaisujen sekä erikoisratkaisun kuvaaja. Miten nämä suhtautuvat toisiinsa? Tarkista väitteesi laskemalla.Tehtävä 18
Johda sen käyräparven differentiaaliyhtälö, johon kuuluvat kaikki xy-tason R-säteiset ympyrät. (Parvella on siis kaksi parametria: ympyrän keskipisteen koordinaatit. R on vakio.) Mitä saatu yhtälö ilmaisee parven käyrien kaarevuussäteistä?Tehtävä 19
Etsi käyräparven y = (1 + C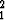
) ln(x + C1) - C1x + C2 differentiaaliyhtälö.
Tehtävä 20
Etsi käyräparven x = C1ey + C2e-y + 3 differentiaaliyhtälö.Tehtävä 21
Johda sen käyräparven differentiaaliyhtälö, johon kuuluvat kaikki x-akselia sivuavat ympyrät.Tehtävä 22
Muodosta tason kaikkien kartioleikkausten (so. toisen asteen käyrien) differentiaaliyhtälö.Tehtävä 23
Muodosta tason kaikkien paraabelien (akselisuunnasta riippumatta) differentiaaliyhtälö.Tehtävä 24
Tutki isokliinien avulla differentiaaliyhtälön y' = x + y ratkaisukäyrien käyttäytymistä.Tehtävä 25
Tutki isokliinien avulla differentiaaliyhtälön xy' = x + y ratkaisukäyrien käyttäytymistä.Tehtävä 26
Olkoot f ja sen osittaisderivaatat fx ja fy jatkuvia. Näytä, että jos yhtälön y' = f(x, y) ratkaisukäyrällä on käännepiste, niin se sijaitsee käyrälläfx(x, y) + fy(x, y)f(x, y) = 0.
Osoita edelleen, että tämän käyrän pisteissä ratkaisukäyrä ja isokliini sivuavat toisiaan.
1.3 Normaaliryhmä
Tehtävä 27
Palauta toisen kertaluvun differentiaaliyhtälö yy'' + xy' = 0 ensimmäisen kertaluvun normaaliryhmäksi Y ' = F (x, Y ). Millainen vektoriarvoinen funktio F on?Tehtävä 28
Kappaleen (planeetan) liikettä keskeisvoimakentässä hallitsee Newtonin lakien mukainen differentiaaliyhtälö
r'' = - a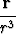
,
missä pilkut tarkoittavat derivaattoja ajan suhteen, r on paikkavektori, r = |r| tämän pituus ja a vakio. Oletetaan tunnetuksi, että kyseessä on tasoliike, jolloin siis r(t) = x(t) i + y(t) j. Hajota differentiaaliyhtälö komponenttifunktioita x(t) ja y(t) koskevaksi kahden yhtälön ryhmäksi ja palauta tämä neljän yhtälön ensimmäisen kertaluvun ryhmäksi ottamalla nopeuskomponentit uusiksi tuntemattomiksi funktioiksi.