2 Tavallisen differentiaaliyhtälön yleisiä ratkaisumenetelmiä
2.1 Ensimmäisen kertaluvun yhtälöt
Tehtävä 30
Ratkaise alkuarvotehtäväy' = -2xy, y(0) = 1.
Piirrä muutama yleisen ratkaisun kuvaaja. Minkä nimisistä käyristä on kyse?
Tehtävä 31
Ratkaise separoimalla differentiaaliyhtälö9yy' + 4x = 0.
Piirrä ratkaisukäyriä.
Tehtävä 32
Ratkaise separoimalla differentiaaliyhtälöy' = 1 + y2.
Tehtävä 33
Ratkaise separoimalla alkuarvotehtävä
y' = -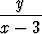 , y(-1) = 1.
, y(-1) = 1.
Tehtävä 34
Ratkaise separoimalla alkuarvotehtävä
y' = 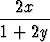 , y(2) = 0.
, y(2) = 0.
Tehtävä 35
Ratkaise alkuarvotehtäväy' + 5x4y2 = 0, y(0) = 1.
Tehtävä 36
Ratkaise alkuarvotehtävä
y' =  , y(1) = 3.
, y(1) = 3.
Tehtävä 37
Määritä seuraavien differentiaaliyhtälöiden yleiset ratkaisut ja piirrä ratkaisukäyrien kuvaajia:| a) x2y' = y2, | b) y' = (1 - y)2, | c) y' = (1 + y)(y - 1), | |||||||||
d) y' = 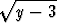 , , | e) (1 + x)y' = 1 + y, | f) 1 + y2 - xy' = 0, | |||||||||
| g) (1 + x3)y' = x2y, | h) (1 - x2)y' = 1 - y2, | i) y' + y2 = 1. |
Tehtävä 38
Ratkaise seuraavat alkuarvoprobleemat:| a) y' = e|x| , y(-1) = -1, | b) y' = sin |x|, y(-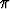 ) = 0, ) = 0, | c) y' 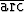 tan y = 1, y(1) = 1, tan y = 1, y(1) = 1, | |||||||||
d) y' sin x = y ln y, y(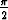 ) = 1, ) = 1, | e) (1 + ex)yy' = ex, y(1) = 1, | f) cos 2x cos(ln y)y' = y, y(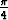 ) = 1. ) = 1. |
Tehtävä 39
Määritä ja piirrä differentiaaliyhtäln y'3 = y yleinen ratkaisu. Onko yhtälöllä erikoisratkaisuja?Tehtävä 40
Ratkaise differentiaaliyhtälö y'2 = 4y. Onko yhtälöllä erikoisratkaisuja? Onko olemassa ehdot y(-1) = 1, y(2) = 1 toteuttavaa ratkaisua?Tehtävä 41
Etsi ne differentiaaliyhtälön y' = 2x|y - 1| ratkaisukäyrät, jotka sivuavat x-akselia.Tehtävä 42
Ratkaise seuraavat differentiaaliyhtälöt:a) (x + y)2y' = 1, b) y' = (2x + y + 3)2, c) y' = cos(x + y).
Tehtävä 43
Ratkaise yhtälö
y' = 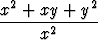 .
.
Tehtävä 44
Ratkaise yhtälöxyy' = x2 + y2.
Tehtävä 45
Määritä seuraavien differentiaaliyhtälöiden ratkaisut tai integraalit ja piirrä ratkaisukäyrien kuvaajia:a) y' = 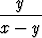 , , | b) y' = 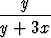 , , | c) y' =  + + 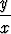 , , | |||||||||
| d) (2x2 + y2)y' = 2xy, | e) xy' = y + x tan  , , | f) xy' = y ln 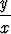 , , | |||||||||
g) 3x(cosh  )y' = 2x sinh )y' = 2x sinh 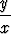 + 3y cosh + 3y cosh 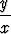 . . |
Tehtävä 46
Ratkaise seuraavat alkuarvoprobleemat:a) xy' = x exp(-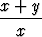 ) + y, y(1) = -1, ) + y, y(1) = -1, | b) y' = 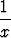 ln ln ![[( ) ]
ey- y
x](kuvat/dy66x.gif) , y(1) = 1, , y(1) = 1, | ||||||
c) y' = 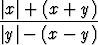 , y(2) = 0. , y(2) = 0. |
Tehtävä 47
Piirrä differentiaaliyhtälön xy' = x + y suuntakenttä. Etsi yhtälön ratkaisu. Piirrä suuntakenttään alkuehdon y(1) = 1 toteuttava ratkaisukäyrä.Tehtävä 48
Etsi yhtälön
(x + x cos 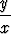 )y' = x + y + y cos
)y' = x + y + y cos 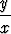
yleinen ratkaisu parametrimuodossa x = x(z), y = y(z).
Tehtävä 49
Totea differentiaaliyhtälö 2xyy' - y2 + x2 = 0 tasa-asteiseksi ja ratkaise se tähän tilanteeseen sopivalla sijoituksella. Mitä mahdetaan tarkoittaa, kun yhtälöä kutsutaan erään ympyräparven differentiaaliyhtälöksi?Tehtävä 50
Olkoon funktio f :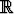
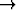
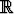 kaikkialla jatkuvasti derivoituva ja
kaikkialla jatkuvasti derivoituva ja 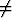 0. Etsi
yhtälön
0. Etsi
yhtälön
f'
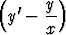 = f
= f
yleinen integraali.
Tehtävä 51
Ratkaise differentiaaliyhtälö eyy' = x + ey - 1 sijoituksella u = x + ey.Tehtävä 52
Piirrä suuntakenttä differentiaaliyhtälölle eyy' = x + ey - 1 ja tähän joitakin ratkaisukäyriä. Ovatko ratkaisukäyrät määriteltyjä kaikilla muuttujan x arvoilla?Tehtävä 53
Ratkaise alkuarvoprobleema eyy' = x + ey - 1, y(0) = a sijoituksella u = x + ey . Mikä ehto vakion a on täytettävä, jotta ratkaisufunktio olisi määritelty kaikilla arvoilla x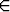
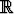 ? Jos a ei täytä tätä ehtoa, funktiolla on singulariteetti jossakin
pisteessä; millaisesta yhtälöstä tämä saadaan? Vrt. laskusi tuloksia edellisen tehtävän
kuvioon.
? Jos a ei täytä tätä ehtoa, funktiolla on singulariteetti jossakin
pisteessä; millaisesta yhtälöstä tämä saadaan? Vrt. laskusi tuloksia edellisen tehtävän
kuvioon.
Tehtävä 54
Ratkaise differentiaaliyhtälö 1 + y2 + xyy' = 0 sopivalla sijoituksella.Tehtävä 55
Tutki seuraavien yhtälöiden muuntumista muuttujien vaihdossa x = ta, y = zb . Valitse vakioille a ja b arvot siten, että yhtälöistä tulee tasa-asteisia ja ratkaise ne.a) 2(x2 - xy2)y' + y3 = 0, b) (x2y2 - 1)y' + 2xy3 = 0.
Tehtävä 56
Ratkaise differentiaaliyhtälöt
a) 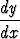 =
= 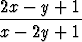 , b)
, b) 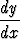 =
= 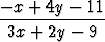 , c)
, c) 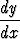 = 2
= 2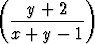 2.
2.
Tehtävä 57
Osoita, että yhtälön(ax + by + c1)y' + bx - ay + c2 = 0
integraalikäyrät ovat logaritmisia spiraaleja.
Tehtävä 58
Osoita differentiaaliyhtälöt| a) 3x2 + 6xy2 + (6x2y + 4y3)y' = 0, | b) e-y + (1 - xe-y)y' = 0, | ||||||
| c) 2x cos 2y + (2y - x2 sin 2y)y' = 0 |
eksakteiksi ja ratkaise ne (muodosta yleiset integraalit). Piirrä suuntakentät ja ratkaisukäyriä.
Tehtävä 59
Totea, että differentiaaliyhtälöllä(3x2 - y2 - 3)y' + 2xy = 0
on integroiva tekijä y2. Ratkaise yhtälö ja piirrä sen ratkaisukäyriä.
Tehtävä 60
Totea, että differentiaaliyhtälö x2y' - 2xy + 3 = 0 ei ole eksakti, mutta siitä voidaan saada eksakti kertomalla se muotoa F (x) olevalla integroivalla tekijällä. Ratkaise yhtälö tällä tavalla.Tehtävä 61
Differentiaaliyhtälöllä(2xy - y2 - y)dx + (2xy - x2 - x)dy = 0
on muotoa F (x + y) oleva integroiva tekijä. Ratkaise yhtälö.
Tehtävä 62
Tarkastellaan differentiaaliyhtälöäP (x, y)dx + Q(x, y)dy = 0.
Osoita, että a) jos (Py - Qx)/Q on pelkästään muuttujan x funktio, niin yhtälöllä on muotoa F (x) oleva integroiva tekijä, b) jos (Py - Qx)/P on pelkästään muuttujan y funktio, niin yhtälöllä on muotoa F (y) oleva integroiva tekijä.
Tehtävä 63
Ratkaise edellisen tehtävän menettelyllä differentiaaliyhtälöt| a) xy2 + y - xy' = 0, | b) - 2xy + (y2 + 3a2 - 3x2)y' = 0, | ||||||
| c) 1 - x2y + x2(y - x)y' = 0, | d) cos y + cos x cos(x + y)y' = 0. |
Tehtävä 64
Etsi ne käyrät, joilla käyrän normaalin ja x-akselin leikkauspisteen etäisyys normaalin kantapisteestä (käyrällä) on vakio a.Tehtävä 65
Määritä ne käyrät, joille y-akselin, käyrän tangentin ja sivuamispisteeseen piirretyn paikkavektorin muodostama kolmio on tasakylkinen.Tehtävä 66
Erään radioaktiivisen aineen hajoamisnopeus on likimain verrannollinen sen määrään. Aineen havaittiin vähentyneen 10 prosenttia 24 tunnissa. Laske puoliintumisaika, so. aika, missä aineen määrä on vähentynyt puoleen alkuperäisestä. Muodosta aluksi differentiaaliyhtälö ainemäärää hetkellä t kuvaavalle funktiolle m(t).Tehtävä 67
Utopian valtakunnassa väestö haluaa sitä vähemmän hyödykkeitä, mitä enemmän se on jo niitä hankkinut. Niinmuodoin elintason nousu on kääntäen verrannollinen jo saavutettuun elintasoon. Tutki, kasvaako elintaso rajatta Utopiassa. Voidaanko tällä mallilla kuvata Utopian elintasoa hamasta muinaisuudesta kaukaiseen tulevaisuuteen?Tehtävä 68
Oletetaan, että syntyvyys populaatiossa on suoraan verrannollinen populaation kokoon ja kuolleisuus keskinäisen kilpailun johdosta suoraan verrannollinen yksilöiden välisten suhteiden (yksilöparien) määrään. Osoita, että tämä johtaa populaatiomalliin
 =
= 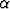 p -
p - 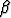 p2,
p2,
missä p on populaation koko ja 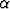 ,
, 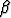 > 0 ovat vakioita. Ratkaise populaation
käyttäytyminen, kun alkuehtona on p(0) = p0. Oletetaan, että
> 0 ovat vakioita. Ratkaise populaation
käyttäytyminen, kun alkuehtona on p(0) = p0. Oletetaan, että 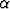 -
- 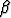 p0 > 0. Onko
populaatiolla maksimikokoa?
p0 > 0. Onko
populaatiolla maksimikokoa?
Tehtävä 69
Säiliössä on 100 litraa suolaliuosta, joka sisältää aluksi 5 kg suolaa. Säiliöön tuodaan nopeudella 5 l/min suolaliuosta, jossa on suolaa 30 g/l. Samalla nopeudella säiliöstä virtaa ulos liuosta. Oletetaan, että liuosta sekoitetaan niin hyvin, että se kaiken aikaa pysyy homogeenisena. Paljonko säiliössä on suolaa tunnin kuluttua?Tehtävä 70
Kappaleen putoamista vastustakoon nopeuden neliöön verrannollinen voima, jolloin nopeus v(t) toteuttaa liikeyhtälön
m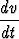 = mg - av2;
= mg - av2;
tässä t on aika, m, g ja a positiivisia vakioita. Ratkaise yhtälö alkuehdolla v(0) = v0 ja
määritä limt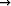
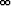 v(t). Mikä on raja-arvon fysikaalinen merkitys?
v(t). Mikä on raja-arvon fysikaalinen merkitys?
Tehtävä 71
Kappaleen jäähtyminen tapahtukoon Newtonin jäähtymislain mukaisesti:
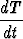 = -k(T - T0),
= -k(T - T0),
missä t on aika, T kappaleen lämpötila, T0 ympäristön muuttumaton lämpötila ja k kappaleelle ominainen vakio. Olkoon k = 0.02s-1 ja T0 = 10o. Olkoon kappaleen lämpötila tarkastelun alkuhetkellä T (0) = 60o. Laske kappaleen lämpötila yhden minuutin, kymmenen minuutin ja tunnin kuluttua.
Tehtävä 72
Laskuvarjohyppääjän nopeutta hidastaa nopeuden neliöön verrannollinen voima, jolloin Newtonin lain mukainen liikeyhtälö on
m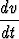 = mg - bv2,
= mg - bv2,
missä v on putoamisnopeus ja t on aika. Ratkaise differentiaaliyhtälö ja osoita, että on
olemassa rajanopeus limt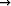
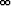 v(t). Määritä rajanopeus, kun hyppääjä painaa m = 80 kg,
hänen nopeutensa varjon auetessa on v0 = 10 m/s, maan vetovoiman kiihtyvyydelle
käytetään arvoa g = 9.8 m/s2 ja hidastuvuuskerroin on b = 30 kg/m. Miten rajanopeus
riippuu hyppääjän alkunopeudesta v0?
v(t). Määritä rajanopeus, kun hyppääjä painaa m = 80 kg,
hänen nopeutensa varjon auetessa on v0 = 10 m/s, maan vetovoiman kiihtyvyydelle
käytetään arvoa g = 9.8 m/s2 ja hidastuvuuskerroin on b = 30 kg/m. Miten rajanopeus
riippuu hyppääjän alkunopeudesta v0?
Tehtävä 73
Tutki, millaisia ratkaisuja on differentiaaliyhtälöllä y'(y(x)) = y(x).Tehtävä 74
Ratkaise integraaliyhtälö
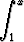
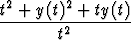 dt = y(x)
dt = y(x)
muodostamalla ensin puolittain derivoimalla differentiaaliyhtälö.
Tehtävä 75
Differentiaaliyhtälön F (x, y, y') = 0 erikoisratkaisut löydetään usein tutkimalla niiden pisteiden (x, y) joukkoa, jotka (jollakin arvolla p) toteuttavat yhtälöt
F (x, y, p) = 0 ja 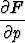 (x, y, p) = 0.
(x, y, p) = 0.
Määritä tämä joukko seuraavien yhtälöiden tapauksessa ja tutki, miten se suhtautuu yleisten ratkaisujen parveen:
a) y'2 + yy' + x = 0, b) y - x + 3y' - y'3 = 0, c) y'2 - yy' + ex = 0.
2.2 Käyräparven leikkaajat
Tehtävä 76
Määritä seuraavien käyräparvien kohtisuorat leikkaajat:| a) y = (x + C)3, | b) x3 - 3xy2 = C, | c) y = Cx exp(x2 + y2), | d) 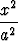 + +  = C, = C, | ||||||||||||
e) 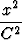 + + 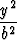 = 1, = 1, | f) 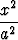 - - 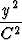 = 1, = 1, | g) y = Cxb. |
Näissä C on parven parametri, muut kirjainsymbolit vakioita. Piirrä kuviot.
Tehtävä 77
Käyrä y = e-x liukuu a) x-akselin, b) y-akselin suunnassa kaikkiin mahdollisiin asemiin. Määritä muodostuneiden käyräparvien kohtisuorat leikkaajat.Tehtävä 78
Määritä sellainen käyrä, joka leikkaa kohtisuorasti sekä parvea y =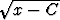 että parvea y = e2x + C.
että parvea y = e2x + C.
Tehtävä 79
Käyräparvi muodostuu paraabeleista, joiden akselina on y-akseli, polttopisteenä origo ja jotka aukeavat ylöspäin. Muodosta parven yhtälö jokin sopiva muuttuja parametrina ja johda parven differentiaaliyhtälö. Etsi kohtisuorien leikkaajien parvi.Tehtävä 80
Käyräparven differentiaaliyhtälö olkoonP (x, y)y'2 + Q(x, y)y' + R(x, y) = 0.
Oletetaan, että alueen G pisteissä derivaatan y' suhteen ratkaistuna yhtälö antaa kaksi eri suurta reaalijuurta. Millä kerroinfunktioita koskevalla ehdolla vastaavat viivaelementit ovat keskenään kohtisuoria? Mikä geometrinen ominaisuus käyräparvella tällöin on?
Tehtävä 81
Määritä napakoordinaateissa annettujen käyräparvien
a) r = C cos 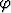 , b) r = C
, b) r = C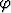 , c) r = Cek
, c) r = Cek
kohtisuorat leikkaajat. Piirrä kuvio.
Tehtävä 82
Määritä parametrimuodossa annetun käyräparven
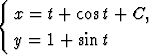
kohtisuorat leikkaajat. (t on käyräparametri, C parviparametri.)
Tehtävä 83
Etsi käyräparvi, joka leikkaa paraabeliparven y2 = 4Cx kulmassa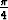 .
.
Tehtävä 84
Käyräparven differentiaaliyhtälö napakoordinaateissa olkoon F (r,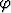 ,
, 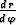 ) = 0.
Mikä on sen parven differentiaaliyhtälö napakoordinaateissa, joka leikkaa em. parven
kulmassa
) = 0.
Mikä on sen parven differentiaaliyhtälö napakoordinaateissa, joka leikkaa em. parven
kulmassa 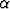 ?
?
2.3 Toisen ja korkeamman kertaluvun yhtälöt
Tehtävä 85
Ratkaise alkuarvoprobleema y'' = x2ex, y(1) = 1, y'(1) = 0.Tehtävä 86
Ratkaise reuna-arvoprobleema y'' = x sin x, y(0) = y(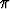 ) = 0.
) = 0.
Tehtävä 87
Palauta toisen kertaluvun differentiaaliyhtälö y'' + y'3ey = 0 ensimmäisen kertaluvun normaaliryhmäksi ja ratkaise se.Tehtävä 88
Ratkaise seuraavat differentiaaliyhtälöt:| a) y''2= y' , | b) y'' = 1 - y'2, | c) xy'' + (x - 1)y' = 0, | d) xy'' = y' ln 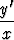 , , | ||||||||||||
| e) y3 y'' = 1, | f) 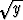 y'' = 1, y'' = 1, | g) y'' = ey, | h) yy'' = 1 + y'2, | ||||||||||||
| i) 2yy'' - 3y' 2 = 4y2, | j) (1 + y2)y'' = y' + y'3. |
Tehtävä 89
Muodosta seuraavia differentiaaliyhtälöitä vastaavat normaaliryhmät ja ratkaise ne:a) y''' = y''3, b) y''' + y''2 = 0, c) y'y''' = 2y''2, d) x2y(4) = 2y'', e) xy(5) = y(4).
Tehtävä 90
Palauta differentiaaliyhtälö yy'' + 2y'2 = 0 ensimmäisen kertaluvun normaaliryhmäksi. Onko ryhmä autonominen? Etsi yhtälön yleinen ratkaisu. Määritä ratkaisukäyrä, joka sivuaa suoraa y = k(x - 1) + 1 pisteessä (1, 1). Piirrä ratkaisukäyrän kuvaajia muuttujan k eri arvoilla.Tehtävä 91
Ratkaise reuna-arvoprobleema(1 - y)y'' + 2y'2 = 0; y(0) = 0, y(-1) = -1.
Onko differentiaaliyhtälöä vastaava normaaliryhmä autonominen?
Tehtävä 92
Määritä ne yhtälön 2y'' = 3y2 integraalikäyrät, joilla on asymptoottina x-akseli.Tehtävä 93
Määritä ne käyrät, joilla kiinteästä muuttujan arvosta laskettu kaarenpituus on suoraan verrannollinen tangentin suuntakulman tangenttiin.Tehtävä 94
Määritä käyrät, joiden kaarevuussäde on
R =  ,
,
missä 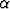 on käyrän tangentin suuntakulma.
on käyrän tangentin suuntakulma.
Tehtävä 95
Osoita, että yhtälö y'' = f(y) voidaan aina ratkaista kahdella integroinnilla.Tehtävä 96
Tarkastellaan differentiaaliyhtälöä y'' = f(y'). a) Osoita, että jos f(a) = 0, niin suorat y = ax + C ovat ratkaisukäyriä. b) Johda integraalikäyrille parametriesitys
x = 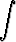
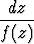 + C1, y =
+ C1, y = 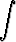
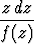 + C2.
+ C2.
Miten ratkaisukäyrät tällöin suhtautuvat toisiinsa?
Tehtävä 97
Tutki seuraavien differentiaaliyhtälötyyppien ratkaisumahdollisuutta integrointien avulla:a) y(n) = f(y(n-1)), b) y(n) = f(y(n-2)).
Tehtävä 98
Olkoon differentiaaliyhtälössä F (x, y, y', . . . , y(n)) = 0 funktiolla F ominaisuus
F (x, ty, ty', . . . , ty(n)) = tkF (x, y, y', . . . , y(n)) kaikilla t 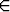
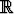 ,
,
missä k on jokin vakio. Mitä tällöin voitetaan sijoituksella u = y'/y? Ratkaise sovellutuksena yhtälö yy''' = y'y''.