4 Differentiaaliyhtälöryhmät
4.1 Ryhmän palauttaminen yhteen yhtälöön
Tehtävä 176
Ratkaise differentiaaliyhtälöryhmät
a) 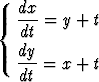 , b)
, b) 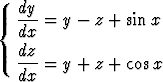 , c)
, c) 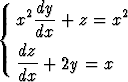 .
.
Tehtävä 177
Etsi yleinen ratkaisu differentiaaliyhtälöryhmälle
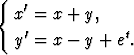
Tehtävä 178
Ratkaise alkuarvoprobleemata) 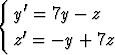 , y(0) = 1, z(0) = 2, , y(0) = 1, z(0) = 2, | |||
b) 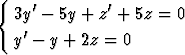 , y(0) = 1, z(0) = 0. , y(0) = 1, z(0) = 0. |
Tehtävä 179
Olkoot x ja y muuttujan t funktioita. Ratkaise alkuarvoprobleema
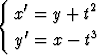 , x(0) = y(0) = 0.
, x(0) = y(0) = 0.
Tehtävä 180
Ratkaise differentiaaliyhtälösysteemi
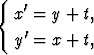
kun alkuehtona on x(1) = y(1) = 2(e - 1). Piirrä ratkaisukäyrät.
Tehtävä 181
Ratkaise kaikilla arvoilla a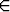
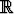 yhtälöryhmät
yhtälöryhmät
a) 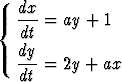 , b)
, b) 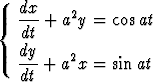 .
.
Tehtävä 182
Etsi differentiaaliyhtälöryhmän x' + y = y' + z = z' + x = 0 yleinen ratkaisu sekä alkuehdon x(0) = y(0) = z(0) = 1 toteuttava yksityisratkaisu.Tehtävä 183
Olkoot x(t), y(t), z(t) ja u(t) tuntemattomia funktioita. Etsi differentiaaliyhtälöryhmän
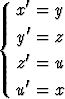
yleinen ratkaisu.
Tehtävä 184
Olkoot x(t), y(t) ja z(t) tuntemattomat funktiot. Ratkaise differentiaaliyhtälöryhmä
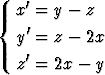
alkuehdolla x(0) = 1, y(0) = 2, z(0) = 3.
Tehtävä 185
Ratkaise: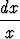 = -
= -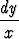 =
= 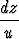 = -
= -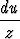 .
.
Tehtävä 186
Olkoot x(t) ja y(t) tuntemattomat funktiot. Etsi yleinen ratkaisu differentiaaliyhtälöryhmälle
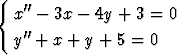 .
.
Tehtävä 187
Olkoot x(t) ja y(t) tuntemattomat funktiot, m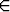
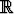 . Etsi yleinen ratkaisu
differentiaaliyhtälöryhmälle
. Etsi yleinen ratkaisu
differentiaaliyhtälöryhmälle
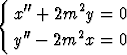 .
.
Tehtävä 188
Palauta Jacobi’n differentiaaliyhtälö
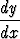 =
= 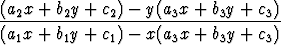
d’Alembertin systeemiksi
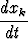 = akx1 + bkx2 + ckx3, k = 1, 2, 3,
= akx1 + bkx2 + ckx3, k = 1, 2, 3,
asettamalla
x(t) = 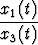 , y(t) =
, y(t) = 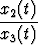 .
.
4.2 Autonomiset ryhmät
Tehtävä 189
Ratkaise autonomiset normaaliryhmät
a) 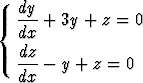 , b)
, b) 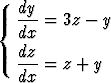 .
.
Ovatko ratkaisujen kuvaajat faasitasossa rajoitettuja?
Tehtävä 190
Ratkaise differentiaaliyhtälöryhmä
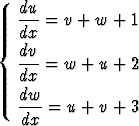 .
.
Tehtävä 191
Olkoot x ja y muuttujan t funktioita, joille pätee
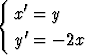 .
.
Millaisia ovat ratkaisukäyrät faasitasossa? Johda näiden yhtälöt.
Tehtävä 192
Johda välttämätön ja riittävä ehto sille, että differentiaaliyhtälöryhmän
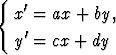
ratkaisussa esiintyy trigonometrisia funktioita. Totea, että ehto bc < 0 on kylläkin välttämätön, mutta ei riittävä.
Tehtävä 193
Heiluri, joka muodostuu painottoman varren (pituus L) päässä olevasta massasta m, saatetaan heilahtelemaan pystysuorassa tasossa. Heilahduskulma olkoon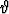 .
Muodosta Newtonin lakien mukainen liikeyhtälö, johda vastaava normaaliryhmä ja totea
se autonomiseksi. Muodosta normaaliryhmästä faasitasokäyrien differentiaaliyhtälö ja
ratkaise se. Piirrä ratkaisukäyrien kuvaajia.
.
Muodosta Newtonin lakien mukainen liikeyhtälö, johda vastaava normaaliryhmä ja totea
se autonomiseksi. Muodosta normaaliryhmästä faasitasokäyrien differentiaaliyhtälö ja
ratkaise se. Piirrä ratkaisukäyrien kuvaajia.
4.3 Lineaarisen vakiokertoimisen ryhmän matriisimuoto
Tehtävä 194
Kirjoita differentiaaliyhtälöryhmä (muuttujana t)
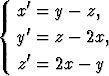
matriisimuotoon ja ratkaise se diagonalisoimalla matriisi.
Tehtävä 195
Ratkaise ominaisarvoteoriaa käyttäen differentiaaliyhtälöryhmä
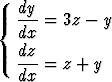 .
.
Tehtävä 196
Ratkaise ominaisarvoteoriaa käyttäen
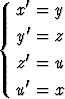 .
.
Tehtävä 197
Etsi differentiaaliyhtälöryhmän
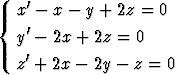 .
.
yleinen ratkaisu sekä alkuehdon x(0) = y(0) = z(0) = 1 toteuttava yksityisratkaisu ominaisarvoteoriaa käyttäen.