6 Differentiaaliyhtälöiden approksimatiivisesta ratkaisemisesta
6.1 Sarjaratkaisut
Tehtävä 201
Ratkaise origokeskisen potenssisarjan avulla differentiaaliyhtälö(1 + x2)y' - 2xy = (1 + x2)2.
Tehtävä 202
Etsi differentiaaliyhtälön y'' - 2y' + y = 0 yleinen ratkaisu origokeskisen potenssisarjan muodossa. Ratkaise differentiaaliyhtälö myös alkeisfunktioiden avulla. Muodosta ratkaisufunktion Maclaurinin sarja. Onko tämä sama kuin edellä saatu sarjaratkaisu?Tehtävä 203
Etsi potenssisarjamuodossa ratkaisu alkuarvoprobleemalle y'' - 2xy' + 2y = 0, y(0) = 1, y' (0) = 0. Määritä sarjan suppenemissäde. Lausu ratkaisu myös alkeisfunktioiden avulla.Tehtävä 204
Etsi differentiaaliyhtälön y'' = y yleinen ratkaisu origokeskisten potenssisarjojen avulla.Tehtävä 205
Etsi origokeskinen sarjaratkaisu Airyn differentiaaliyhtälölle y'' - xy = 0.Tehtävä 206
Etsi origokeskinen sarjaratkaisu differentiaaliyhtälölle(1 - x2)y'' - 2xy' + 6y = 0.
Totea, että yhtälöllä on yksityisratkaisuna polynomi.
Tehtävä 207
Etsi alkuarvoprobleemalle y' = x2 - y2, y(0) =
potenssisarjaratkaisu. Tutki
sarjan suppenemissädettä numeerisesti ja piirrä saadun sarjaratkaisun kuvaaja.
Tehtävä 208
Määritä edellisen tehtävän potenssisarja, kun alkuehtona on a) y(0) = 0, b) y(0) = 1. Piirrä laskemasi osasumman kuvaaja. Ratkaise sama alkuarvoprobleema myös numeerisesti ja piirrä saadun numeerisen ratkaisun kuvaaja.Tehtävä 209
Laske approksimaatioita edellisen tehtävän alkuehtoja vastaavien potenssisarjojen suppenemissäteille. Riippuuko suppenemissäde alkuehdosta? Voidaanko suppenemissäde jotenkin päätellä edellisen tehtävän kuvaajista?6.2 Numeerisesta ratkaisemisesta
Tehtävä 210
Ratkaise numeerisesti Eulerin menetelmällä alkuarvoprobleema a) y' = y, y(0) = 1, b) y' = -y, y(0) = 1. Valitse askelpituudeksi h = 0.2 ja tarkasteluväliksi [0, 5]. Vertaa tulosta tarkkaan ratkaisuun. Millä tavalla a- ja b-kohta ovat tarkkuuden suhteen erilaisia?Tehtävä 211
Ratkaise numeerisesti Eulerin menetelmällä alkuarvoprobleema y' = 2xy + 1, y(0) = 1. Valitse a) h = 0.1, b) h = 0.01. Piirrä ratkaisukäyrät välillä [0, 1]. Muodosta myös yhtälön tarkka ratkaisu.Tehtävä 212
Ratkaise numeerisesti Eulerin menetelmällä alkuarvoprobleema y' = |y - 1|, y(0) = 0. Laske y(3). Käytä eri askelpituuksia. Muodosta myös yhtälön tarkka ratkaisu.Tehtävä 213
Ratkaise alkuarvoprobleema y' = y, y(0) = 1 numeerisesti välillä [0, 5] a) Eulerin menetelmällä, b) Runge – Kutta -algoritmilla. Valitse askelpituudeksi h = 0.1. Piirrä tarkan ratkaisun ja numeeristen ratkaisujen kuvaajat.Tehtävä 214
Kirjoita differentiaaliyhtälöä y'' + xy' + y = 0 vastaava ensimmäisen kertaluvun normaaliryhmä. Muodosta tämän perusteella Eulerin menetelmän mukaiset numeeriset ratkaisukaavat, kun alkuehdot ovat y(0) = 1, y'(0) = 2.Tehtävä 215
Differentiaaliyhtälö
= 
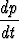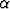p - 
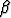p2
esittää erästä populaatiomallia; tässä p on populaation koko ja 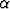, 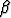> 0 ovat
vakioita. Olkoon 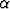= = 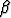10 ja p0 = 0.1. Muodosta Eulerin menetelmän mukainen
iteraatiokaava differentiaaliyhtälön numeerista ratkaisemista varten. Ratkaise
yhtälö käyttäen askelpituuksia h = 0.18, h = 0.23, h = 0.25, h = 0.30. Havainto?
Tehtävä 216
Tutki alkuarvoprobleeman y' = 2xy, y(0) = 1 numeerista ratkaisemista Eulerin menetelmällä. Laske y(5) käyttämällä askelpituuksia h = 1, h = 0.5 ja h = 0.1.Tehtävä 217
Ratkaise alkuarvoprobleema
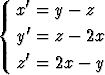, x(0) = 1, y(0) = 2, z(0) = 3
numeerisesti. Piirrä saatujen ratkaisukäyrien kuvaajat.
Tehtävä 218
Piirrä alkuarvotehtävän y' = (1 + x)y + 1 - 3x + x2, y(0) = 0.06 ratkaisukäyrät käyttäen sekä Eulerin että Rungen–Kuttan menetelmiä. Käytä askelpituutta h = 0.04. Ohjelmoi menetelmät itse. Havaintoja?Tehtävä 219
Määritä y(1.5) ja piirrä funktion y = y(x) kuvaaja välillä [0, 1.5], kun funktio y on alkuarvotehtävän y' = y2 - cos x, y(0) = 1 ratkaisu. Käytä Rungen–Kuttan menetelmää ja askelpituutta h = 0.1. Onko yhtälö ratkaistavissa alkeisfunktioiden avulla? Voiko sen ratkaista symbolisesti laskentaohjelmalla?Tehtävä 220
Piirrä Rungen–Kuttan menetelmällä alkuarvoprobleeman y' = x - y2, y(0) = 0 ratkai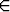su välillä x
[0, 300]. Käytä askelpituutta 0.1. Havaintosi? Puolita
askelpituus ja piirrä kuvaaja uudelleen. Entä jos tällä puolitetulla askelpituudella
piirrettäisiinkin ratkaisu välillä x 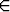[0, 1000]? Mikä voisi olla selityksenä havaituille
ilmiöille?
Tehtävä 221
Tutki laskentaohjelma avulla differentiaaliyhtälön y' = x2 - y2 yleistä ratkaisua. Pyri erityisesti selvittämään, miten käyttäytyvät ne yksittäisratkaisut, jotka toteuttavat alkuehdot a) y(0) = 0, b) y(0) = 1. Tarkastele sekä symbolista (algebrallista) että numeerista ratkaisemista.Tehtävä 222
Tutki alkuarvoprobleeman y' = x - y2, y(0) = 0 numeerista ratkaisua Eulerin menetelmällä välillä [0, 200] ja Rungen – Kuttan menetelmällä välillä [0, 500]. Käytä kummassakin tapauksessa kiinteää askelpituuutta h = 0.1. Osaatko selittää syntyvän ilmiön?Tehtävä 223
Tutki alkuarvoprobleeman y' = x - y2, y(0) = a ratkaisuja kokeellisesti antamalla vakiolle a erilaisia arvoja ja ratkaisemalla yhtälö numeerisesti laskentaohjelmalla. Määritä kolmen desimaalin tarkkuudella sellainen arvo, jonka eri puolilla ratkaisut käyttäytyvät oleellisesti eri tavoin. Tutki, onko olemassa ratkaisua, joka jää eri tavoin käyttäytyvien ratkaisujen väliin. Löydätkö tarkan arvon vakion a kriittiselle arvolle?Tehtävä 224
Tutkitaan differentiaaliyhtälön y' = x - y2 ratkaisua alkuehdoilla y(0) = 3, y(0) = 1, y(0) = 0, y(0) = -0.7 ja y(0) = -0.75. Piirrä nämä alkuehdot toteuttavien ratkaisukäyrien kuvaajat samaan kuvaan välillä x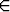 [0, 9]. Sopiva y-akselin väli on [-3, 3].
Havaintosi? Mitä tällainen tilanne voisi tarkoittaa, jos kokeellisesti (jossain mittauksessa)
olisi saatu alkuarvo y(0) = -0.75?
6.3 Approksimointi funktioilla
Tehtävä 225
Etsi approksimaatio alkuarvoprobleeman y' = xy, y(0) = 1 ratkaisulle Picardin – Lindelöfin menettelyllä. Valitse aloitusfunktioksi vakiofunktio y0(x) = 1. Vertaa tulosta tarkan ratkaisun Maclaurinin polynomiin.Tehtävä 226
Tarkastellaan alkuarvoprobleemaa y' = f(x, y) = 2x + 5y, y(0) = 0. Osoita, että funktio f täyttää tasaisen Lipschitzin ehdon. Laske probleeman ratkaisulle Picardin – Lindelöfin menetelmän mukaiset approksimaatiot yk(x), k = 1, 2, 3, 4, kun valitaan y0 (x) = 0.Tehtävä 227
Laske Picardin – Lindelöfin menettelyllä approksimoivia polynomeja alkuarvoprobleeman y' = x2 - y2, y(0) = 1 ratkaisulle.Tehtävä 228
Alkuarvoprobleeman y' = f(x, y), y(x0) = y0 ratkaisua voidaan approksimoida funktiojonolla, joka muodostetaan rekursiolla
y0 (x) = y0 = vakio; yn+1(x) = y0 +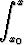 
f(x, yn(x)) dx, n = 0, 1, 2, 3, . . . .
Approksimoi tällä tavoin alkuarvoprobleeman y'' + xy = 0, y(0) = 0, y'(0) = 1 ratkaisua. Differentiaaliyhtälö on ensin kirjoitettava normaaliryhmän muotoon Y ' = F (x, Y ), missä Y ja F ovat vektoriarvoisia funktioita. Laske funktiojonon alkupään termejä ja vertaa niiden antamaa approksimaatiota alkuarvoprobleeman tarkkaan ratkaisuun (joka on lausuttavissa Airyn funktioiden avulla).