Sisällön pääryhmät Alkeisfunktiot Logaritmifunktio [ 1 2 3 4 ] ESITIEDOT:  reaalifunktiot,  eksponenttifunktio KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Eksponentti- ja logaritmiyhtälöitä saattaa olla mahdollista ratkaista laskusääntöjä käyttäen. Yleensä ne kuitenkin ovat sellaisia transkendenttiyhtälöitä, joissa ainoa mahdollisuus on numeerinen ratkaiseminen esimerkiksi Newtonin iteraatiota käyttäen.

1) Yhtälö

4^x + 4^-x = 5/2

voidaan ratkaista kertomalla se ensin tekijällä 4^x, jolloin saadaan toisen asteen yhtälö tuntemattomana 4^x:

(4^x)² - 4^x + 1 = 0.

Tällä on juuret 4^x = 2 ja 4^x = . Ottamalla kummastakin puolesta 2-kantainen logaritmi saadaan x = ja x = -.

2) Yhtälö

log_x2 + 2 = log_x(1 - x)

voidaan logaritmin laskusääntöjen avulla sieventää muotoon

log_x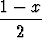 = 2.

Jotta esiintyvä x-kantainen logaritmifunktio olisi määritelty, on ilmeisestikin oltava x > 0, x1 ja 1 - x > 0.

Ottamalla kummastakin puolesta x-kantainen eksponenttifunktio saadaan toisen asteen yhtälö (1 - x) = x². Tämän juuret ovat x = -1 ja x = , joista vain jälkimmäinen täyttää määrittelyehdot. Ainoa ratkaisu on siis x = 1/2.

eksponenttifunktio  yhtälö (transkendentti-)  Newtonin iteraatio  yhtälö (toisen asteen)

Kivelä, niinkuin matematiikka, versio 1.12