Sisällön pääryhmät Potenssit ja polynomit Polynomien tekijöihin jako [ 1 2 3 4 ] ESITIEDOT:  polynomit,  reaaliluvut,  kompleksiluvut KATSO MYÖS:  polynomiyhtälöt

Kansisivu  Sisältö  Hakemisto

Kysymys yhden muuttujan polynomin tekijöihin jaosta voidaan ratkaista polynomiyhtälöiden teorian avulla. Jos nimittäin

p(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀

on astetta n oleva polynomi, jonka nollakohdat, so. polynomiyhtälön p(x) = 0 ratkaisut ovat x₁,  x₂,  ...,  x_n, voidaan kirjoittaa

p(x) = a_n(x - x₁)(x - x₂)...(x - x_n),

jolloin polynomi on tullut jaetuksi ensimmäistä astetta oleviin tekijöihin. Menettely perustuu ns. algebran peruslauseeseen.

Jos kaikki nollakohdat ovat reaalisia, tekijöihin jako onnistuu reaalialueella; jos joukossa on kompleksilukuja, jako on mahdollinen vain kompleksialueella.

Esimerkiksi: Toisen asteen yhtälön x² - 2x - 1 = 0 juuret ovat x₁ = 1 + ja x₂ = 1 - 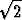. Nämä ovat siis polynomin x² - 2x - 1 nollakohdat ja tekijöihin jaoksi saadaan

x² - 2x - 1 = (x - x₁)(x - x₂) = [x - (1 + 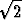)][x - (1 - )].

Kuudennen asteen polynomin x⁶ + 1 kaikki nollakohdat ovat

x1 = 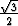+ ,	x2 = i,	x3 = - + ,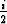
x4 = -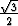 - 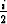,	x5 = -i,	x6 = - .

Tekijöihin jako kompleksialueella on tällöin

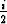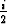x⁶ + 1 = (x - i)(x + i)(x + - )(x + + )(x - - )(x - + ),

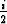mistä päästään reaalialueen tekijöihin kertomalla aina kaksi perättäistä tekijää keskenään:

x⁶ + 1 = (x² + 1)(x² + x + 1)(x² - x + 1).

Menettely pätee kaikille reaalikertoimisille polynomeille, koska näiden kompleksiset nollakohdat muodostavat aina liittolukupareja.

yhtälö (polynomi-)  algebran peruslause  reaaliluku  kompleksiluku  yhtälö (toisen asteen)  liittoluku

Kivelä, niinkuin matematiikka, versio 1.12