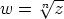 , kun
, kun  on annettu. Yhtälö voidaan kirjoittaa
muotoon
on annettu. Yhtälö voidaan kirjoittaa
muotoon 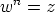 , missä
, missä 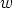 on tuntematon. Napakoordinaattiesitysten
on tuntematon. Napakoordinaattiesitysten
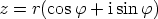 ja
ja 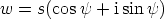 avulla yhtälö saa muodon
avulla yhtälö saa muodon
Olkoon laskettavana 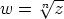 , kun
, kun  on annettu. Yhtälö voidaan kirjoittaa
muotoon
on annettu. Yhtälö voidaan kirjoittaa
muotoon 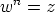 , missä
, missä 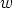 on tuntematon. Napakoordinaattiesitysten
on tuntematon. Napakoordinaattiesitysten
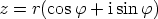 ja
ja 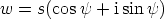 avulla yhtälö saa muodon
avulla yhtälö saa muodon
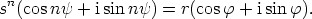
Tällöin tulee olla 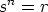 ja
ja 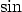 - ja
- ja 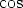 -funktioiden jaksot huomioon ottaen
-funktioiden jaksot huomioon ottaen
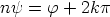 , missä
, missä 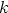 on kokonaisluku. Näistä seuraa
on kokonaisluku. Näistä seuraa
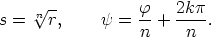
Koska 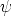 on kompleksiluvun napakulma, riittää tarkastella niitä luvun
on kompleksiluvun napakulma, riittää tarkastella niitä luvun 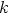 arvoja, jotka antavat napakulman yhden kierroksen alueelta. Helpointa
on rajoittaa jaksotermi
arvoja, jotka antavat napakulman yhden kierroksen alueelta. Helpointa
on rajoittaa jaksotermi 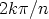 välille
välille 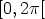 , ts. tarkastella arvoja
, ts. tarkastella arvoja
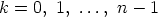 . Näitä vastaten juurelle
. Näitä vastaten juurelle 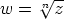 saadaan
saadaan 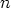 arvoa:
arvoa:
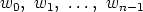 .
.
Juuret voidaan kirjoittaa muotoon
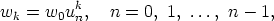
missä 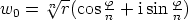 ja
ja 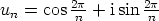 on kiertotekijä.
on kiertotekijä.
Juuret sijaitsevat tasavälisesti sellaisen ympyrän kehällä, jonka säde on 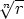 .
Kertomalla edellinen juuri kiertotekijällä päästään seuraavaan juureen.
.
Kertomalla edellinen juuri kiertotekijällä päästään seuraavaan juureen.
Jos 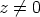 , sillä on
, sillä on 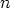 eri suurta juurta. Näistä jokin määritellään juuren
pääarvoksi. Laskentaohjelmissa tämä on yleensä se, jolla on itseisarvoltaan pienin
napakulma.
eri suurta juurta. Näistä jokin määritellään juuren
pääarvoksi. Laskentaohjelmissa tämä on yleensä se, jolla on itseisarvoltaan pienin
napakulma.
Linkkejä
Kompleksilukujen tulo ja potenssit
Kiertotekijä
Kompleksiluvun juuren laskeminen (esimerkki)
Simo K. Kivelä 27.04.2005