 ,
,
Yleisen teorian mukaan ensimmäisen kertaluvun epähomogeenisen yhtälön y' + P0(x)y = R(x) yleinen ratkaisu saadaan lisäämällä vastaavan homogeeniyhtälön y' + P0(x)y = 0 yleiseen ratkaisuun jokin epähomogeenisen yhtälön yksittäisratkaisu.
Ratkaiseminen tapahtuu siten kahdessa vaiheessa: Ensin etsitään vastaavan homogeeniyhtälön ratkaisu, joka on muotoa y = Cy1(x). Tämän jälkeen haetaan jokin — mikä tahansa — epähomogeeniyhtälön ratkaisu.
Epähomogeeniyhtälön yksittäisratkaisu voidaan usein löytää arvaamalla sen periaatteellinen muoto ja sijoittamalla yhtälöön vastaava yrite.
Myös yleinen menettely on olemassa, mutta se saattaa johtaa hankaliin laskuihin. Yleistä menettelyä kutsutaan vakion varioinniksi, koska yritteenä käytetään homogeeniyhtälön yleisestä ratkaisusta saatavaa lauseketta, jossa vakio C on korvattu (ts. sitä ’varioidaan’) tuntemattomalla funktiolla u: yrite on siten y = u(x)y1(x). Tuntematon funktio u pyritään määräämän siten, että yrite toteuttaa yhtälön.
Kun yrite ja sen derivaatta y' = u'y1 + uy1' sijoitetaan differentiaaliyhtälöön ja termit ryhmitetään sopivasti, saadaan
u(y1' + P0y1) + u'y1 = R.
Koska y1 toteuttaa homogeeniyhtälön, on vasemman puolen ensimmäinen termi = 0 ja jäljelle jää yhtälö
u' = 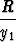 ,
,
josta u saadaan yhdellä integroinnilla.
Integroimisvakiota ei tarvitse ottaa huomioon, koska tavoitteena on löytää vain jokin yksittäisratkaisu, ts. vain jokin funktio u.
Etsitty yksittäisratkaisu on siis u(x)y1(x).