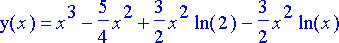
| rtkalk.mws |
Olkoon annettuna differentiaaliyhtälö alkuehtoineen:
> diffyht:= x^2*diff(y(x), x, x)-3*x*diff(y(x), x)+4*y(x)=x^3;
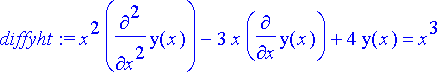
> ehto1:= y(2)=3;
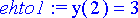
> ehto2:= D(y)(2)=4;

Yleinen ratkaisu saadaan dsolve -komennolla.
> ratkaisu:= dsolve(diffyht, y(x));
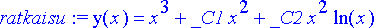
Määritellään ratkaisu funktioksi Y( x ). Tällöin vakiot _ C1 ja _ C2 saadaan ratkaistua tekemällä ensin merkkikorvaus y -> Y edellä annetuille ehdoille ja käyttämällä niitä solve -komennon argumentteina.
> Y:= unapply(rhs(ratkaisu), x);
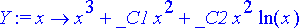
>
subs(y=Y, {ehto1, ehto2}):
C12:= solve(%, {_C1, _C2});
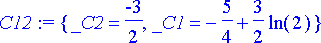
Sijoittamalla vakiot yleiseen ratkaisuun saadaan alkuehtoa vastaava yksittäisratkaisu:
> y0:= subs(C12, rhs(ratkaisu));
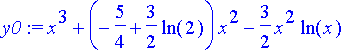
Tämä toteuttaa differentiaaliyhtälön ja alkuehdot:
>
subs(y(x)=y0, {diffyht}):
simplify(%);
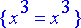
>
subs(x=2, y0);

> subs(x=2, diff(y0,x));
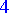
Alkuehdot voidaan yhtälön ohella antaa dsolve -komennolle, jolloin yksittäisratkaisu saadaan suoraan:
>
ratkaisu:= dsolve({diffyht, y(2)=3, D(y)(2)=4}, y(x)):
simplify(%);