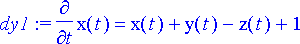
| ryhsym.mws |
Olkoon tarkasteltavana kolmen differentiaaliyhtälön normaalimuotoinen ryhmä, jossa tuntemattomina funktioina ovat x( t ), y( t ) ja z( t ):
>
dy1:= diff(x(t), t)=x(t)+y(t)-z(t)+1;
dy2:= diff(y(t), t)=-x(t)+5*y(t)+z(t)+t;
dy3:= diff(z(t), t)=-2*x(t)+2*y(t)+4*z(t)+t^2;
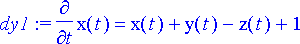
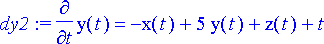
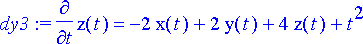
> funktiot:= [x(t), y(t), z(t)];
![funktiot := [x(t), y(t), z(t)]](Images/ryhsym4.gif)
Ryhmä pyritään ratkaisemaan eliminoimalla ensin yhtälöistä funktiot x ja y , jolloin saadaan yksinomaan funktiota z koskeva differentiaaliyhtälö. Tätä varten kaksi ensimmäistä yhtälöä derivoidaan kerran ja viimeinen yhtälö kaksi kertaa, jolloin saadaan kaikkiaan seitsemän yhtälöä:
>
dy4:= diff(dy1, t):
dy5:= diff(dy2, t):
dy6:= diff(dy3, t):
dy7:= diff(dy3, t$2):
dy1, dy2, dy3, dy4, dy5, dy6, dy7;
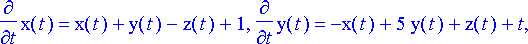
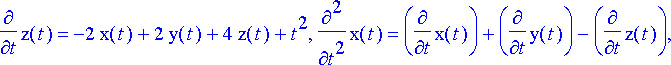
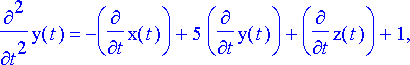
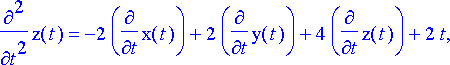
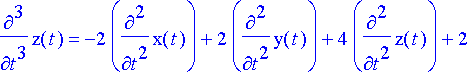
Kuudesta ensimmäisestä yhtälöstä voidaan ratkaista funktiot x ja y derivaattoineen ja tämän jälkeen sijoittaa lausekkeet perättäin viimeiseen yhtälöön.
Määritellään ensin tuntemattomat:
> tuntemattomat:=[diff(y(t), t, t), diff(x(t), t, t), diff(x(t), t), diff(y(t), t), y(t), x(t)];
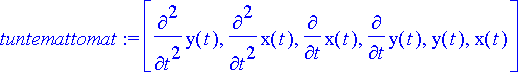
Ratkaistaessa Maple n solve -komennolla ei ole mahdollista ratkaista derivaattojen suhteen, jos derivaatasta esiintyy useampia kertalukuja. Tämä voidaan ohittaa korvaamalla derivaatta- ja funktiomerkinnät väliaikaisilla muuttujilla.
>
d2m:= zip((x, y)->x=y, tuntemattomat, [seq(d[k], k=1..6)]):
m2d:= zip((x, y)->x=y, [seq(d[k], k=1..6)], tuntemattomat):
>
subs(d2m, [{dy1, dy2, dy3, dy4, dy5, dy6}, tuntemattomat]):
solve(%[1], {%[2][]}):
elimsij:= subs(m2d, %);
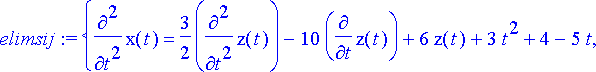
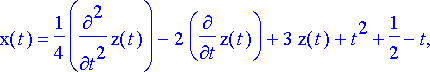
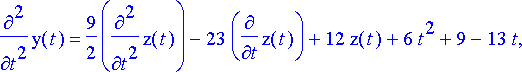
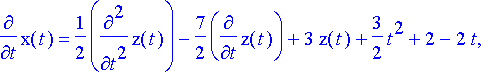
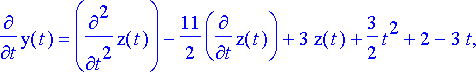
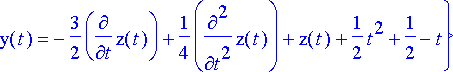
> dy:= subs(elimsij, dy7);
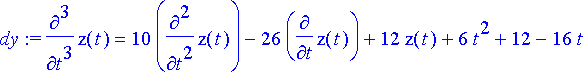
Tuloksena on kolmannen kertaluvun yhtälö funktiolle z . Tämä voidaan löytää myös hieman suorempaan käyttämällä Maple n eliminate -komentoa. Myös eliminate -komennon käyttö vaatii edellä esitellyt korvaustoimenpiteet.
>
subs(d2m, [{dy1, dy2, dy3, dy4, dy5, dy6, dy7}, tuntemattomat]):
eliminate(%[1], {%[2][]}):
op(subs(m2d, %)[-1])=0;
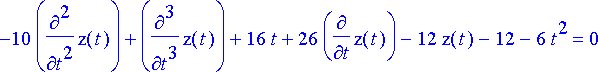
Yhtälön ratkaisuksi saadaan
> zratk:= dsolve(dy, z(t));
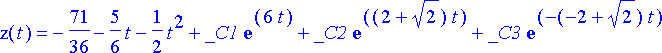
Yhtälöryhmän yleinen ratkaisu muodossa x( t ), y( t ), z( t ) saadaan tätä ja aiempia lausekkeita käyttäen:
>
subs(elimsij, funktiot):
ylratk:= subs(zratk, %):
simplify(%);
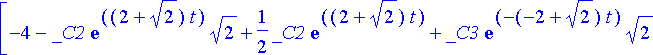
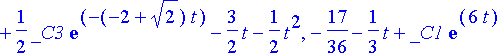
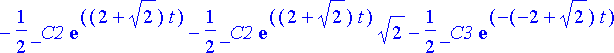
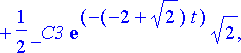
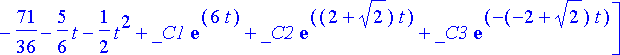
Tiettyä alkuehtoa vastaavat vakioiden arvot saadaan tämän jälkeen tavalliseen tapaan ratkaisemalla algebrallinen yhtälöryhmä. Olkoon alkuehtona x(0) = 1, y(0) = -2, z(0) = 3. Tällöin
>
subs(t=0, ylratk):
vakiot:= solve({%[1]=1, %[2]=-2, %[3]=3}, {_C1, _C2, _C3}):
simplify(%);
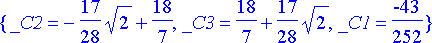
Vastaava yksittäisratkaisu saadaan sijoittamalla vakioiden arvot yleiseen ratkaisuun:
>
yksittratk:= subs(vakiot, ylratk):
simplify(%);
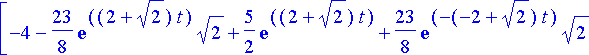

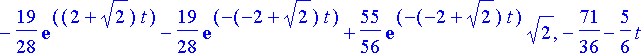
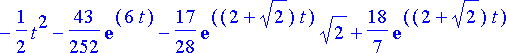
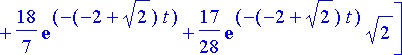
Ratkaisujen kuvaajat:
> plot(yksittratk, t=0..1, view=[0..1, -20..20], color=red);
![[Maple Plot]](Images/ryhsym32.gif)
Edellä oleva esitys kuvaa, miten eliminointiprosessi ja yhtälöryhmän ratkaiseminen tapahtuu. Jos tavoitteena on ainoastaan saada tietyn alkuarvoprobleeman ratkaisu, päästään paljon vähemmällä kohdistamalla Maple n dsolve -funktio suoraan alkuperäiseen yhtälöryhmään ja alkuehtoon:
>
suoraratk:= dsolve({dy1, dy2, dy3, x(0)=1, y(0)=-2, z(0)=3},funktiot):
simplify(%);
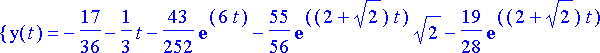
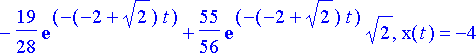
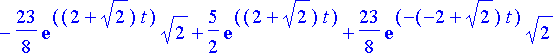
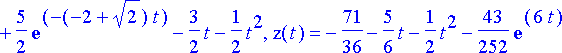
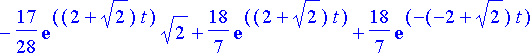
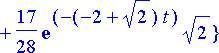
Eri tavoilla saadut ratkaisut ovat todellakin samat:
>
subs(suoraratk, [x(t), y(t), z(t)]):
zip((x, y)->simplify(x-y), %, yksittratk);
![[0, 0, 0]](Images/ryhsym39.gif)