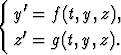
Toisinaan — varsinkin käsinlaskussa — normaalimuodossa oleva differentiaaliyhtälöryhmä on järkevää muuntaa yhdeksi korkeampaa kertalukua olevaksi differentiaaliyhtälöksi ja samalla eliminoida tuntemattomat funktiot yhtä lukuunottamatta. Tämän jälkeen voidaan yrittää ratkaista saatu yhtälö jollakin yhtä yhtälöä koskevalla menettelyllä. Kyseessä on käänteinen menettely normaaliryhmän muodostamiselle.
Kahden yhtälön ryhmän
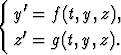
tapauksessa eliminointia varten derivoidaan jompikumpi ryhmän yhtälöistä, jolloin saadaan kolme yhtälöä; esimerkiksi
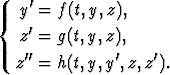
Viimeinen yhtälö on saatu derivoimalla ryhmän jälkimmäinen yhtälö muuttujan t suhteen, jolloin oikealle puolelle ilmestyy funktioiden y ja z derivaatat.
Saaduista kolmesta yhtälöstä eliminoidaan y ja y' algebrallisesti — jos voidaan. Tämä voi tapahtua ratkaisemalla kahdesta yhtälöstä y ja y' sekä sijoittamalla saadut funktiosta z riippuvat lausekkeet kolmanteen yhtälöön. Tuloksena saadaan toisen kertaluvun yhtälö funktiolle z.
Vastaavaa menettelyä voidaan soveltaa myös isommissa ryhmissä. Jos yhtälöitä on n kappaletta, yksi niistä derivoidaan n - 1 kertaa ja muut n - 2 kertaa, jolloin saadaan kaikkiaan n + (n - 1)2 = n2 - n + 1 yhtälöä. Yhdestä tuntemattomasta funktiosta esiintyy tällöin derivaatat kertalukuun n saakka. Muut tuntemattomat funktiot ja niiden derivaatat (kertalukuun n - 1 saakka) voidaan tällöin ainakin periaatteessa eliminoida. Näiden lukumäärä on nimittäin (n - 1)n = n2 - n, so. yhtä pienempi kuin yhtälöiden lukumäärä. Menettely johtaa kuitenkin yleensä algebrallisiin vaikeuksiin paitsi lineaarisen yhtälöryhmän tapauksessa. Tällöinkään se ei ole järkevä, koska parempiakin ratkaisutapoja on olemassa.