 P(x) dx
P(x) dx
Lineaarinen epähomogeeninen ensimmäisen kertaluvun differentiaaliyhtälö y' + P (x)y = R(x) voidaan ratkaista integroivan tekijän menettelyllä.
Kertomalla yhtälö tekijällä
M(x) = e P(x) dx
P(x) dx
ja siirtelemällä termejä se saadaan muotoon ![[M (x)P (x)y - M (x)R(x)]](kuvat/esim74x.gif) + M(x)y' = 0.
Tämän kerroinfunktioille pätee
+ M(x)y' = 0.
Tämän kerroinfunktioille pätee

![[M (x)P (x)y - M (x)R(x)]](kuvat/esim76x.gif) = M(x)P (x) =
= M(x)P (x) = 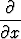 M(x).
M(x).
Yhtälö on siis eksakti ja M(x) on integroiva tekijä.
Ratkaisu on tällöin löydettävissä muodossa F (x, y) = C, missä
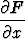 = M(x)P (x)y - M(x)R(x) ja
= M(x)P (x)y - M(x)R(x) ja 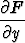 = M(x).
= M(x).
Integroimalla jälkimmäinen yhtälö muuttujan y suhteen saadaan F (x, y) = M(x)y + g(x), missä g(x) on integroimisvakio. Edellisestä yhtälöstä seuraa tämän jälkeen
M(x)P (x)y + g'(x) = M(x)P (x)y - M(x)R(x) eli g'(x) = -M(x)R(x),
ja funktio g(x) saadaan yhdellä integroinnilla.
Yhdistämällä saadut tulokset ja kirjoittamalla tekijän M(x) lauseke paikoilleen saadaan yhtälö F (x, y) = C muotoon
ye P(x) dx -
P(x) dx - 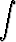 R(x)e
R(x)e P(x) dx dx = C.
P(x) dx dx = C.
Ratkaisemalla tästä y saadaan yhtälön yleinen ratkaisu:
y = Cy1(x) + y1(x)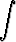
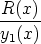 dx,
dx,
missä on merkitty
y1(x) = e- P(x) dx.
P(x) dx.
Lukija verratkoon tätä vakion varioinnilla saatavaan ratkaisuun!