Toisen kertaluvun yhtälön muuntaminen normaaliryhmäksi ja ratkaiseminen separoimalla

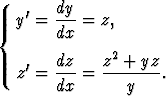
Autonomista toisen kertaluvun differentiaaliyhtälöä yy'' = y'² + yy' vastaava normaaliryhmä on

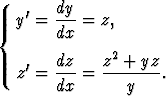
Jos yhtälöt jaetaan puolittain ja differentiaaliosamäärämerkinnöistä supistetaan dx pois, päädytään yhtälöön

= ,

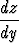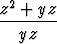joka riippuu vain muuttujista y ja z. Sitä voidaan siis pitää differentiaaliyhtälönä, joka määrää näiden välisen riippuvuuden.

Sijoituksella u(y) = z(y)/y yhtälö voidaan palauttaa separoituvaksi. Koska z = uy, on 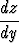= y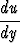 + u. Tällöin yhtälö saa muodon

y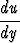 + u = u + 1  eli  du = .

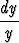Integroimalla puolittain saadaan u = ln|C₁y|, jolloin integroimisvakio on kirjoitettu muotoon ln |C₁|. (Miksi näin voidaan tehdä rajoittamatta vakion arvoja?) Koska u = z/y, saadaan muuttujien y ja z väliseksi riippuvuudeksi z = y ln|C₁y|. Kyseessä on normaaliryhmän ratkaisujen faasitasoesitysten yhtälö.

Normaaliryhmän ensimmäisen yhtälön mukaan on nyt

y' = 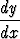= y ln|C₁y|,

mikä on jälleen separoituva yhtälö. Separoimalla saadaan

dx =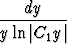

ja puolittain integroimalla

x + C₂ = ln|ln|C₁y||.

Ratkaisemalla y:n suhteen ja sieventämällä saadaan alkuperäisen differentiaaliyhtälön yleinen ratkaisu

y = D₁e^D₂ex ,

missä on otettu käyttöön uudet vakiot D₁ = 1/C₁ ja D₂ = ±e^C₂.