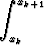 f(x, y(x)) dx.
f(x, y(x)) dx.
Integroimalla differentiaaliyhtälö y' = f(x, y(x)) puolittain välin [xk, xk+1] yli saadaan
y(xk+1) - y(xk) = 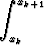 f(x, y(x)) dx.
f(x, y(x)) dx.
Kun funktion y arvot korvataan niiden approksimaatioilla ja integraalin arvioimiseen käytetään puolisuunnikassääntöä, päädytään kaavaan
yk+1 = yk + 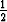 h
h![[f (xk,yk) + f(xk+1,yk+1)]](kuvat/ratk48x.gif) .
.
Tämä ei suoranaisesti anna mahdollisuutta differentiaaliyhtälön numeeriseen ratkaisemiseen, koska yk+1 esiintyy myös kaavan oikealla puolella.
Kaavaa voidaan kuitenkin soveltaa siten, että arvolle yk+1 lasketaan ensin karkeampi approksimaatio tavallisella Eulerin menetelmällä ja tätä käytetään eo. kaavan oikealla puolella. Kaavaa käytetään siis karkean arvon tarkentamiseen.
Laskeminen tapahtuu kahdessa vaiheessa:
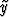 k+1 k+1 | = yk + hf(xk, yk), | ||
| yk+1 | = yk + 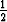 h h![[f(xk,yk) + f(xk+1,y~k+1)]](kuvat/ratk51x.gif) . . |
y' = f(x, y), y(x0) = y0
ratkaisun toisen asteen Taylorin kehitelmä pisteessä xk on
| y(xk + h) | = y(xk) + hy'(xk) +  y''(xk)h2 + O(h3) y''(xk)h2 + O(h3) | ||
= y(xk) + ![[hf (x ,y(x )) + 1h2(f (x ,y(x )) + f (x ,y(x ))f (x ,y(x )))]
k k 2 x k k y k k k k](kuvat/ratk53x.gif) + O(h3). + O(h3). |
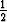 h
h![[f (x ,y(x )) + f(x + h,y(x ) + hf (x ,y(x )))]
k k k k k k](kuvat/ratk55x.gif) .
.
Tämä johtaa samaan kaksivaiheiseen kaavaan kuin edellä.