Monisilmukkainen vaihtovirtapiiri

Otetaan tarkastelun kohteeksi RLC-vaihtovirtapiiri jossa on käämejä, vastuksia ja kondensaattoreita.

Kytkentä 1

Tarkastellaan virtapiiriä, jossa yksinkertaiseen RLC-piiriin on kodensaattorin rinnalle kytketty piiri, jossa on vastus ja toinen kondensaattori. Alla kuva piirin kokoonpanosta.

Piirin komponentit kohdistavat jännitteeseen kolme erilaista pudotusta,

käämin yli,

vastuksen yli sekä

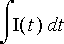kondensaattorin yli.

Lisäksi piiriin syötetään sinimuotoista vaihtovirtaa . Muodostetaan yllä olevalle piirille differentiaaliyhtälöt kiertämällä piiriä virtasilmukoiden ja muodostamia silmukoita myöden. Kirchhoffin lain mukaan molempien virtojen kulkiessa komponentin yli tapahtuu jännitteen muutos. Saadaan yhtälöt

,

.

Jotta integraalitermeistä päästään eroon, yhtälöt derivoidaan:

,

.

Tämä on differentiaaliyhtälöryhmä pakotetulle värähtelylle. Ratkaistaan yhtälöt ja siten virrat virtasilmukoissa 1 ja 2.

Laskujen aluksi on syytä hävittää mahdollisista aiemmista laskuista jääneet muuttujat:

> restart;

Määritellään yhtälöryhmä ja sen tuntemattomat.

> ryhma:= L[1]*diff(i[1](t), t$2)+R[1]*diff(i[1](t), t)+(i[1](t)-i[2](t))/C[1]=E[0]*omega*cos(omega*t), i[2](t)/C[2]+(-i[1](t)+i[2](t))/C[1]+R[2]*diff(i[2](t), t)=0;

> tuntemattomat:= {i[1](t), i[2](t)};

Sijoitetaan vakioille arvot ja asetetaan alkuehto. Kytkettävä lähde on verkkovirtalähde ja sitä ennen piirissä ei ollut virtaa.

> ryhma1:= subs({L[1]=0.1, R[1]=5, C[1]=0.001, R[2]=3, C[2]=0.0005, E[0]=230, omega=2*Pi*50}, {ryhma});

> alkuehto:= i[1](0)=0, D(i[1])(0)=0, i[2](0)=0;

Ratkaistaan yhtälöryhmä numeerisin laskentamenetelmin.

> rtk:= dsolve({ryhma1[], alkuehto}, tuntemattomat, type=numeric, output=listprocedure);

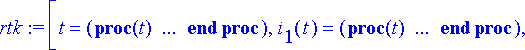
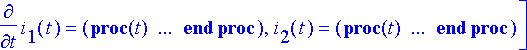
Poimitaan ratkaisusta virtaa kuvaavat termit.

> virrat:= subs(rtk, [i[1](t), i[2](t)]):

Piirretään kuvaaja virralle piirin eri osissa. Sininen käyrä on jaetun kondensaattorin läpi kulkeva virta, punainen käyrä on virtakierroksen 1 virta ja vihreä virtakierroksen 2 virta.

> with(plots):

Warning, the name changecoords has been redefined

> display(plot(virrat[1]-virrat[2], 0..0.2, color=blue),
plot(virrat[1], 0..0.2, color=red),
plot(virrat[2], 0..0.2, color=green));

Vaihtovirta näyttää jakautuvan hieman eri vaiheisena rinnakkaisten kondensaattorien kesken. Alkuehdon aikaansaama epävakaisuus näyttää vaimenevan varsin nopeasti.

Kytkentä 2

Tarkastellaan seuraavaksi RLC-virtapiiriä, jossa käämin rinnalle on kytketty sama vastus ja kondensaattori kuin edellä. Alla kuva piirin kokoonpanosta.

Huomaa virtakierrosten valinta! Pyrimme pitämään laskennan helpottamiseksi yhtälöryhmän kertaluvun mahdollisimman alhaalla virtakierrosvalinnoilla. Kirchhoffin lain perusteella saatavat yhtälöt ovat derivoidussa muodossa.

,

.

Muodostetaan yhtälöryhmä ja tuntemattomat:

> ryhma:= L[1]*diff(i[1](t), t$2)+R[1]*(diff(i[1](t), t)+diff(i[2](t), t))+(i[1](t)+i[2](t))/C[1]=E[0]*omega*cos(omega*t), R[1]*(diff(i[2](t), t)+diff(i[2](t), t))+(i[1](t)+i[2](t))/C[1]+R[2]*diff(i[2](t), t)+i[2](t)/C[2]=E[0]*omega*cos(omega*t);

> tuntemattomat2:= {i[1](t), j[2](t)};

Muodostetaan alkuehto ja annetaan vakioille arvot. Kytkettävä lähde on verkkovirtalähde ja sitä ennen piirissä ei ollut virtaa. Vakiot ovat samat kuin edellä.

> ryhma2:= subs({L[1]=0.1, R[1]=5, C[1]=0.001, R[2]=3, C[2]=0.0005, E[0]=230, omega=2*Pi*50}, {ryhma});

> alkuehto:= i[1](0)=0, D(i[1])(0)=0, i[2](0)=0;

Ratkaistaan yhtälöryhmä numeerisesti.

> rtk2:= dsolve({ryhma2[], alkuehto}, tuntemattomat, type=numeric, output=listprocedure);

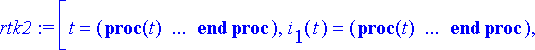
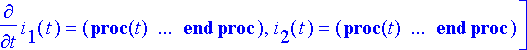
> virrat:= subs(rtk2, [i[1](t), i[2](t)]):

Yhtälöryhmän ratkaiseminen dsolve -komennolla symbolisesti on myös mahdollista, mutta tämän on hyvin hidasta ja sieventämisessä joudutaan helposti vaikeuksiin.

Piirretään kuvaaja virralle piirin eri osissa. Punainen käyrä on jaetun käämin läpi kulkeva virta, vihreä virtakierroksen 2 virta ja sininen on näiden summavirta.

> display(plot(virrat[1], 0..0.2, color=red),
plot(virrat[2], 0..0.2, color=green),
plot(virrat[1]+virrat[2], 0..0.2, color=blue));

Tuloksesta näkyy, miten käämi pyrkii vastustamaan virran muutosta ja sen läpi kulkeva virta on hyvin vähäinen. Vastaavasti se indusoi jopa primääripiiriä voimakkaamman värähtelyn lisäyspiiriin.

Tehtävä

Tarkastellaan vielä alla kuvattua piiriä, jossa on samanaikaisesti molemmat edellä tarkastellut lisäkytkennät.

Muodosta kolmen differentiaaliyhtälön ryhmä yllä esitetylle piirille. Käytä apuna kuvaan piirrettyjä virtakierroksia. Piirrä kuvaajat virran kululle eri komponenteissa. Vihje: Olet oikeilla jäljillä, mikäli virtakierron 3 värähtely on vastakkaisvaiheista kiertojen 1 ja 2 kanssa.