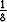Yhtälön derivointi ja integrointi

Differentiaaliyhtälö voidaan puolittain derivoida tai integroida. Sellaisenaan tämä ei useinkaan johda yhtälön ratkaisemiseen, mutta auttaa muuttamaan probleeman toisenlaiseen, ehkä helpompaan muotoon tai saamaan osittaista informaatiota ratkaisuista.

Esimerkiksi:

1) Olkoon tarkasteltavana alkuarvoprobleema y'' + xyy' = 0, y(2) = 3, y'(2) = 5.

Derivoimalla differentiaaliyhtälö saadaan y''' + yy' + xy'² + xyy'' = 0. Koska sekä tämä että alkuperäinen yhtälö ovat voimassa kaikilla muuttujan arvoilla, ne erityisesti ovat voimassa alkuehtopisteessä x = 2. Tällöin on

Alkuperäisen yhtälön derivointi kuitenkin hävittää informaatiota: yhtälössä olisi saanut olla lisäksi mikä tahansa vakiotermi, ja derivoitu yhtälö olisi ollut sama. Täten ei ole selvää, että saadut funktiot y ovat myös alkuperäisen yhtälön ratkaisuja.

Sijoittamalla lausekkeet alkuperäiseen yhtälöön todetaan, että tulee olla A = 0 ja B = 2C² . Alkuperäisen yhtälön ratkaisut ovat siten y = -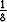x² ja y = Cx + 2C², C mielivaltainen vakio. Edellinen on yhtälön erikoisratkaisu, jälkimmäinen yleinen ratkaisu.

3) Jos alkuarvoprobleemassa y' = f(x, y), y(x₀) = y₀ differentiaaliyhtälö integroidaan puolittain välin [x₀, x] yli, saadaan

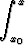y'(x) dx = 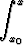f(x, y(x)) dx     eli     y(x) = y₀ + 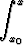f(x, y(x)) dx.

Oikean puolen integraalia ei voida laskea, koska se sisältää tuntemattoman funktion y(x). Yhtälö on kuitenkin saatu muunnetuksi uuteen muotoon: se ei sisällä enää tuntemattoman funktion derivaattaa, mutta kylläkin integraalin, jonka sisällä tuntematon funktio on. Tällaista yhtälöä sanotaan integraaliyhtälöksi.