![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Yhtälöt ja epäyhtälöt
Yhtälöt ja epäyhtälöt  Juuriyhtälöt [ 1 2
]
Juuriyhtälöt [ 1 2
]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) yhtälöt,
yhtälöt, ![[#]](kuvat/msam10-c-4.gif) juuret
juuret
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt
polynomiyhtälöt
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Yhtälöt ja epäyhtälöt Yhtälöt ja epäyhtälöt  Juuriyhtälöt [ 1 2
] Juuriyhtälöt [ 1 2
]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) yhtälöt, yhtälöt, ![[#]](kuvat/msam10-c-4.gif) juuret juuret
KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt polynomiyhtälöt
|
|
Esimerkkinä olkoon yhtälön
 =
=  +
+ 
reaalisten juurten ratkaiseminen. Puolittainen neliöön korotus antaa
x = x + 1 + x + 2 + 2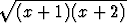 .
.
Sieventämällä siten, että jäljellä oleva neliöjuuri jää yksinään toiselle puolelle, saadaan
-x - 3 = 2 .
.
Uuden neliöön korotuksen jälkeen ei juurta enää esiinny:
x2 + 9 + 6x = 4(x + 1)(x + 2)
ja on päädytty toisen asteen yhtälöön
3x2 + 6x - 1 = 0,
jonka juuret ovat x = -1 ± 
 . Likiarvot ovat x1
. Likiarvot ovat x1  0.15470 ja x2
0.15470 ja x2  -2.15470.
-2.15470.
Näistä jälkimmäinen ei kelpaa, koska ratkaisun tulee olla > 0; alkuperäisen yhtälön vasen puoli ei ole muuten reaalinen. Edellinen antaa yhtälön termeille likiarvot

 0.39332,
0.39332, 
 1.07457,
1.07457, 
 1.46789,
1.46789,
joten on ilmeistä, että myöskään x1 ei ole alkuperäisen yhtälön ratkaisu.
Yhtälöllä ei ole siten ratkaisuja lainkaan, mikä olisi ollut melko helposti nähtävissä
jo alkuperäisestä yhtälöstäkin: Koska x < x + 1, on myös  <
< 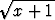 ja sitäkin
suuremmalla syyllä
ja sitäkin
suuremmalla syyllä  <
<  +
+  . Sama tulos olisi ollut helposti
nähtävissä piirtämällä yhtälön kummankin puolen kuvaajat. Saaduille
likiarvoille pätee 0.39332 = -1.07457 + 1.46789, jolloin x1 on yhtälön
. Sama tulos olisi ollut helposti
nähtävissä piirtämällä yhtälön kummankin puolen kuvaajat. Saaduille
likiarvoille pätee 0.39332 = -1.07457 + 1.46789, jolloin x1 on yhtälön
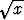 = -
= - +
+  ratkaisu. Tämä on luonnollistakin, koska tästä yhtälöstä
päädytään neliöön korotusten jälkeen juuri samaan toisen asteen yhtälöön kuin
edellä.
ratkaisu. Tämä on luonnollistakin, koska tästä yhtälöstä
päädytään neliöön korotusten jälkeen juuri samaan toisen asteen yhtälöön kuin
edellä.
![[#]](kuvat/msam10-c-4.gif) sieventäminen (yhtälön) sieventäminen (yhtälön)![[#]](kuvat/msam10-c-4.gif) neliöjuuri neliöjuuri![[#]](kuvat/msam10-c-4.gif) yhtälö (toisen asteen) yhtälö (toisen asteen)![[#]](kuvat/msam10-c-4.gif) kuvaaja kuvaaja |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12