Sisällön pääryhmät Derivaatta Nopeus ja kiihtyvyys [ 1 2 ] ESITIEDOT:  derivaatta KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Keskinopeus v on kuljettu matka s jaettuna vastaavalla ajalla t:

v = .

Lähtöhetken jälkeen kuljettu matka on ajan funktio: s = s(t). Kulkunopeuden ei tarvitse olla vakio. Aikaväliä [t, t + t] vastaava matka on tällöin s = s(t + t) - s(t) ja keskinopeus siis

v = .

Jos tarkastellaan yhä lyhyempää aikaväliä, ts. t 0, saadaan hetkellinen nopeus hetkellä t:

v(t) = lim_t0 = s'(t).

Hetkellinen nopeus on siis kuljetun matkan derivaatta ajan suhteen.

Kyseessä voi olla muukin kuin kulkunopeus. Esimerkiksi vesisäiliötä täytettäessä vesimäärän tilavuus muuttuu ajan mukana: V = V (t). Keskimääräinen täyttymisnopeus aikavälillä [t, t + t] on tilavuuden muutos jaettuna vastaavalla ajalla:

;

esimerkiksi tietty määrä kuutiometrejä sekunnissa. Jos t 0, tästä saadaan hetkellinen täyttymisnopeus

lim_t0 = V '(t).

Yleisesti: Ajan mukana muuttuvan suureen muuttumisnopeus on sen derivaatta ajan suhteen.

Kiihtyvyys tarkoittaa nopeuden v muuttumisnopeutta. Keskikiihtyvyys aikavälillä [t, t + t] on siten

a =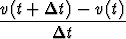

ja hetkellinen kiihtyvyys a(t) = v'(t). Jos kyseessä on liikkuva kappale, jonka kulkema matka on s(t), on siis a(t) = s''(t).

erotusosamäärä  derivaatta  derivaatta (toinen)

Kivelä, niinkuin matematiikka, versio 1.12