Sisällön pääryhmät Derivaatta Nopeus ja kiihtyvyys [ 1 2 ] ESITIEDOT:  derivaatta KATSO MYÖS:

Kansisivu  Sisältö  Hakemisto

Pallonmuotoista ilmapalloa täytetään kokoonpuristumattomalla kaasulla, joka virtaa vakionopeudella 0.5 dm³/s. Millä nopeudella pallon säde kasvaa sillä hetkellä, kun säteen suuruus on 20 cm?

Sekä pallon säde että tilavuus ovat ajan t funktioita:

V (t) = r(t)³.

Derivoimalla ajan suhteen yhdistetyn funktion derivoimissääntöä käyttäen saadaan

V '(t) = 4r(t)²r'(t).

Tässä V '(t) on tilavuuden kasvunopeus ja r'(t) säteen kasvunopeus. Esimerkkitapauksessa tunnetaan kaasun virtausnopeus, ts. pallon tilavuuden kasvunopeus ja saadaan siis

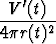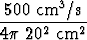
r'(t) = = 1 mm/s.

pallo  pallo (tilavuus)  pallo (ala)  derivaatta (yhdistetyn funktion)  derivointi (alkeisfunktioiden)

Kivelä, niinkuin matematiikka, versio 1.12