![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Alkeisfunktiot
Alkeisfunktiot  Trigonometrian kaavat [ 1
2 3 4 5 6 ]
Trigonometrian kaavat [ 1
2 3 4 5 6 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot
trigonometriset funktiot
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Alkeisfunktiot Alkeisfunktiot  Trigonometrian kaavat [ 1
2 3 4 5 6 ] Trigonometrian kaavat [ 1
2 3 4 5 6 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) trigonometriset funktiot trigonometriset funktiot
KATSO MYÖS: |
|
Kaksinkertaisen argumentin kaavat saadaan asettamalla sinin ja kosinin yhteenlaskukaavoihin y = x ja käyttämällä kosinin tapauksessa hyväksi peruskaavaa muodossa sin2x = 1 - cos2x ja cos2x = 1 - sin2x:
| sin 2x | = | 2 sin x cos x |
| cos 2x | = | cos2x - sin2x = 1 - 2 sin2x = 2 cos2x - 1 |
Harvemmin tarvittavia ovat seuraavat kaavat:
| sin x + sin y | = | 2 sin 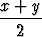 cos cos  |
| sin x - sin y | = | 2 cos 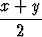 sin sin  |
| cos x + cos y | = | 2 cos 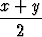 cos cos  |
| cos x - cos y | = | -2 sin  sin sin  |
Nämä saadaan johdetuiksi sinin ja kosinin yhteenlaskukaavojen avulla seuraavaan tapaan: Laskemalla yhteen kaavat
sin( + +  ) ) | = | sin  cos cos  + cos + cos  sin sin  , , | ||
sin( - -  ) ) | = | sin  cos cos  - cos - cos  sin sin  |
sin( +
+  ) + sin(
) + sin( -
-  ) = 2 sin
) = 2 sin  cos
cos  .
.
Sijoittamalla tähän x =  +
+  ja y =
ja y =  -
-  , jolloin
, jolloin  =
=  (x + y) ja
(x + y) ja
 =
=  (x - y), päädytään ryhmän ensimmäiseen kaavaan. Muut saadaan
vastaavasti.
Kaksinkertaisen kulman kosinin kaavoista cos 2x = 1 - 2 sin2x ja cos 2x = 2 cos2x - 1
saadaan sinin ja kosinin neliöt ratkaisemalla
(x - y), päädytään ryhmän ensimmäiseen kaavaan. Muut saadaan
vastaavasti.
Kaksinkertaisen kulman kosinin kaavoista cos 2x = 1 - 2 sin2x ja cos 2x = 2 cos2x - 1
saadaan sinin ja kosinin neliöt ratkaisemalla
| sin2x | = |  (1 - cos 2x) (1 - cos 2x) |
| cos2x | = |  (1 + cos 2x) (1 + cos 2x) |
![[#]](kuvat/msam10-c-4.gif) sini sini![[#]](kuvat/msam10-c-4.gif) kosini kosini |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12