Kahden yhtälön ryhmän ratkaiseminen yhteen yhtälöön palauttamalla

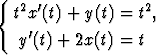
Differentiaaliyhtälöryhmästä

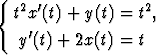
voidaan muodostaa vain funktiota y koskeva yhtälö derivoimalla ryhmän jälkimmäinen yhtälö ja eliminoimalla saaduista kolmesta yhtälöstä x ja x'. Yhtälöryhmä ei tosin ole normaalimuodossa, mutta tällä ei ole merkitystä.

Derivoinnilla saatava kolmen yhtälön ryhmä on

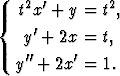
Kahdesta viimeisestä ratkaisemalla saadaan

x = 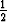(t - y'),   x' = 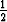(1 - y''),

ja kun nämä sijoitetaan ensimmäiseen yhtälöön, päädytään toisen kertaluvun yhtälöön

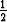t²(1 - y'') + y = t²  eli  t²y'' - 2y = -t².

Itse asiassa funktiota x ei edes tarvitse sijoittaa, mutta periaatteessa ensimmäinen yhtälö olisi saattanut sisältää myös tällaisen termin.

Funktiolle y on siten saatu toisen kertaluvun lineaarinen epähomogeeninen yhtälö. Vastaava homogeeniyhtälö on Eulerin yhtälö. Menetelmät yhtälön ratkaisemiseen ovat siis olemassa ja ratkaisuksi saadaan

y = C₁t² + 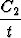- t² ln|t|.

Toinen tuntematon funktio x saadaan tämän jälkeen helposti:

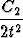x = (t - y') = ( - C₁)t + + t ln|t|.

Periaatteessa funktio x voitaisiin ratkaista myös derivoimalla alkuperäisen yhtälöryhmän ensimmäinen yhtälö ja eliminoimalla täten saaduista kolmesta yhtälöstä funktio y. Tuloksena olisi toisen kertaluvun lineaariyhtälö funktiolle x. Tämän ratkaiseminen johtaisi lausekkeeseen, jossa on kaksi uutta integroimisvakiota, esimerkiksi D₁ ja D₂ .

Ratkaisuun tulisi siis kaikkiaan neljä vakiota: C₁, C₂, D₁, D₂. Kuitenkin edellä saadussa ratkaisussa funktioiden x ja y lausekkeissa on vain kaksi riippumatonta vakiota, C₁ ja C₂. Selityksenä on, että vakiot C₁, C₂, D₁, D₂ eivät ole toisistaan riippumattomia, vaan niiden välillä on side-ehtoja, jotka eivät paljastu, jos tuntemattomat funktiot etsitään toisistaan riippumattomasti.