Sisällön pääryhmät Funktio Funktiokäsite [ 1 2 3 4 5 6 ] ESITIEDOT: KATSO MYÖS:  reaalifunktiot,  joukko-oppi

Kansisivu  Sisältö  Hakemisto

Funktion f : A B maalijoukon B jokaisen alkion ei tarvitse olla lähtöjoukon jonkin alkion kuva. Ne maalijoukon alkiot, jotka todella ovat kuvia, muodostavat kuvajoukon; tätä merkitään f(A). Samalle kuvajoukon alkiolle voi kuvautua useampiakin lähtöjoukon alkioita.

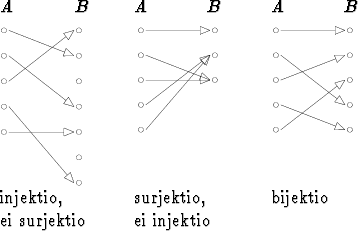
Jos kuvajoukko on sama kuin maalijoukko, ts. jokainen maalijoukon alkio on ainakin yhden alkion kuva, sanotaan, että funktio on surjektio.

Jos jokainen maalijoukon alkio on enintään yhden alkion kuva, funktiota sanotaan injektioksi.

Jos jokainen maalijoukon alkio on täsmälleen yhden alkion kuva, ts. funktio on sekä surjektio että injektio, sanotaan, että se on bijektio. Bijektiossa siis jokaista lähtöjoukon alkiota vastaa yksi maalijoukon alkio ja kääntäen.

Esimerkiksi: Olkoon reaalilukujoukko ja ₊ ei-negatiivisten reaalilukujen joukko. Jos f(x) = x², niin

f : ei ole surjektio eikä injektio,

f : + on surjektio, mutta ei injektio,

f : + ei ole surjektio, mutta on injektio,

f : + + on sekä surjektio että injektio, ts. bijektio.

joukko  alkio

Kivelä, niinkuin matematiikka, versio 1.12