![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Funktio
Funktio  Funktiokäsite [ 1 2 3 4 5 6
]
Funktiokäsite [ 1 2 3 4 5 6
]
ESITIEDOT:
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) reaalifunktiot,
reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) joukko-oppi
joukko-oppi
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Funktio Funktio  Funktiokäsite [ 1 2 3 4 5 6
] Funktiokäsite [ 1 2 3 4 5 6
]
ESITIEDOT: KATSO MYÖS: ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot, reaalifunktiot, ![[#]](kuvat/msam10-c-4.gif) joukko-oppi joukko-oppi
|
|
1) Olkoon A kaikkien Suomen kansalaisten joukko ja B sellaisten 11 merkin jonojen joukko, jotka ovat muodollisesti oikeita henkilötunnuksia. Sääntö, joka jokaiseen Suomen kansalaiseen liittää hänen henkilötunnuksensa, on funktio.
2) Olkoon A = B =  (reaalilukujoukko). Funktio f : A
(reaalilukujoukko). Funktio f : A  B voidaan
määritellä asettamalla f(x) = x2, jolloin jokaiseen reaalilukuun x liitetään sen
neliö.
B voidaan
määritellä asettamalla f(x) = x2, jolloin jokaiseen reaalilukuun x liitetään sen
neliö.
3) Olkoon A reaalilukujoukko kuten edellä, mutta B ei-negatiivisten reaalilukujen
joukko (merkitään usein B =  +). Funktio f : A
+). Funktio f : A  B määritellään samoin kuin
edellä: f(x) = x2. Vaikka sääntö onkin sama, pidetään tätä eri funktiona kuin
edellisessä kohdassa, koska maalijoukko on valittu eri tavoin.
B määritellään samoin kuin
edellä: f(x) = x2. Vaikka sääntö onkin sama, pidetään tätä eri funktiona kuin
edellisessä kohdassa, koska maalijoukko on valittu eri tavoin.
4) Olkoon A = B = 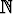 (luonnollisten lukujen joukko). Funktio f : A
(luonnollisten lukujen joukko). Funktio f : A  B voidaan
määritellä myös seuraavasti:
B voidaan
määritellä myös seuraavasti:
| f(1) = 1, |
| f(2) = 1, |
| f(n) = f(n - 1) + f(n - 2), kun n > 3. |
Määrittelyä kutsutaan rekursiiviseksi, koska esimerkiksi f(5) on määritelty arvojen f(4) ja f(3) avulla ja nämä on edelleen palautettava arvoihin f(2) ja f(1). (Funktion f arvoja kutsutaan Fibonacci’n luvuiksi.)
5) Olkoon lähtöjoukkona xy-taso, ts. reaalilukuparien joukko. Tällöin merkitään
A =  2. Maalijoukko olkoon B =
2. Maalijoukko olkoon B =  . Määritellään funktio f : A
. Määritellään funktio f : A  B, joka
jokaiseen xy-tason pisteeseen liittää erään lukuarvon: f(x, y) = x2 - y2. Tämä on
esimerkki kahden muuttujan funktiosta.
B, joka
jokaiseen xy-tason pisteeseen liittää erään lukuarvon: f(x, y) = x2 - y2. Tämä on
esimerkki kahden muuttujan funktiosta.
6) Vastaavaan tapaan voidaan määritellä usean muuttujan funktio f :  n
n 
 asettamalla vaikkapa f(x1, x2, . . . , xn) = x
asettamalla vaikkapa f(x1, x2, . . . , xn) = x + x
+ x + . . . + x
+ . . . + x . Tässä on
n > 1.
. Tässä on
n > 1.
7) Olkoon A =  ja olkoon B kolmiulotteisten vektoreiden joukko. Yhtälö
ja olkoon B kolmiulotteisten vektoreiden joukko. Yhtälö
r(t) = cos t i + sin t j + t k
määrittelee tällöin vektoriarvoisen funktion r : A  B. Funktion voidaan katsoa
esittävän ruuviviivaksi kutsuttua avaruuskäyrää.
B. Funktion voidaan katsoa
esittävän ruuviviivaksi kutsuttua avaruuskäyrää.
![[#]](kuvat/msam10-c-4.gif) joukko joukko![[#]](kuvat/msam10-c-4.gif) reaaliluku reaaliluku![[#]](kuvat/msam10-c-4.gif) luonnollinen luku luonnollinen luku![[#]](kuvat/msam10-c-4.gif) rekursiivisesti määritelty lukujono rekursiivisesti määritelty lukujono![[#]](kuvat/msam10-c-4.gif) koordinaatisto (xy-) koordinaatisto (xy-)![[#]](kuvat/msam10-c-4.gif) vektori vektori![[#]](kuvat/msam10-c-4.gif) ruuviviiva ruuviviiva![[#]](kuvat/msam10-c-4.gif) käyrä (avaruus-) käyrä (avaruus-) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12