Sisällön pääryhmät Derivaatta Käyrän kuperuus [ 1 2 ] ESITIEDOT:  reaalifunktiot,  derivaatta KATSO MYÖS:  derivointisäännöt,  alkeisfunktioiden derivaatat,  maksimit ja minimit

Kansisivu  Sisältö  Hakemisto

Piste, jossa käyrän kuperuussuunta vaihtuu, on käännepiste.

Oheinen kuvio esittää polynomin p(x) = x⁵ - x⁴ - x³ + x² + 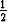käännepisteet.

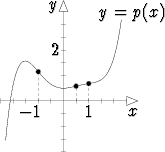
Koska käyrä ei käännepisteessä ole kupera ylöspäin eikä myöskään alaspäin, on käännepiste välttämättä toisen derivaatan nollakohta. Toisella derivaatalla voi kuitenkin olla muitakin nollakohtia. Käännepisteiden x-koordinaatit ovat siten yhtälön f''(x) = 0 ratkaisujen joukossa, mutta kaikki ratkaisut eivät välttämättä liity käännepisteisiin.

Tilanne on vastaavanlainen kuin ensimmäisen derivaatan tapauksessa: Yhtälö f'(x) = 0 antaa mahdolliset ääriarvokohdat, yhtälö f''(x) = 0 mahdolliset käännepisteet.

Jotta piste olisi käännepiste, täytyy toisen derivaatan merkin muuttua kohtaa ohitettaessa.

Esimerkki: Funktioilla x³ ja x⁴ on origossa toisen derivaatan nollakohta. Edellisellä origo on käännepiste, jälkimmäisellä ei.

käyrä (taso-)  polynomi  derivaatta (toinen)  ääriarvokohta

Kivelä, niinkuin matematiikka, versio 1.12