Sisällön pääryhmät Kulma, kolmio, monikulmio ja -tahokas Monikulmiot [ 1 2 3 4 5 ] ESITIEDOT:  kolmio KATSO MYÖS:  geometriset probleemat

Kansisivu  Sisältö  Hakemisto

Monikulmioksi kutsutaan tasokuviota, jota rajaa perättäisten janojen muodostama monikulmion piiri. Janat ovat monikulmion sivuja, niiden päätepisteet monikulmion kärkipisteitä. Jos kärkipisteitä (ja siis myös sivuja) on n kappaletta, puhutaan n-kulmiosta. Perättäisten sivujen väliin jäävät monikulmion kulmat.

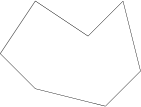
Jokainen n-kulmio voidaan kärkipisteet sopivasti yhdistämällä jakaa n - 2 kolmioksi, mistä seuraa, että n-kulmion kulmien summa on (n - 2) ^. 180^o.

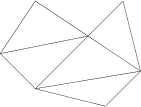
Janaa, joka yhdistää kaksi monikulmion kärkeä, mutta joka ei ole monikulmion sivu, kutsutaan sen lävistäjäksi. Jokaisesta n-kulmion kärjestä voidaan siten piirtää n - 3 lävistäjää. Kertomalla tämä kärkien lukumäärällä ja jakamalla kahdella (koska jokainen lävistäjä yhdistää kaksi kärkeä), saadaan lävistäjien kokonaismäärä: n(n - 3).

jana  kulma (taso-)  kolmio

Kivelä, niinkuin matematiikka, versio 1.12