Sisällön pääryhmät Potenssit ja polynomit Potenssi [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  juuret,  reaalifunktiot,  kompleksiluvut

Kansisivu  Sisältö  Hakemisto

Potenssin määritelmä voidaan yleistää myös negatiivisille luvuille ja kompleksiluvuille. Monet matemaattiset tietokoneohjelmat esimerkiksi antavat seuraavanlaisia tuloksia:

(-1)1/3 0.5000 + 0.8660i,

(-1) -0.9027 - 0.4303i,

ii 0.2079,

missä i tarkoittaa imaginaariyksikköä. Näiden tarkat arvot ovat

(1 + i),  cos(²) + i sin(²),  e^-/2.

Määrittelyn perustana on Eulerin kaava ja potenssiinkorotussäännön säilyminen:

(cos + i sin ) = (eⁱ) = eⁱ = cos() + i sin().

Tällöin on esimerkiksi

(-1)^1/3 = (eⁱ)^1/3 = e^i/3 = cos + i sin = (1 + i).

Huomattakoon, että arvo (-1)^1/3 = (1 + i) on itse asiassa ristiriidassa reaalialueelle luonnollisemman määrittelyn kanssa: (-1)^1/3 = = -1.

Kompleksilukujen murto- ja irrationaalipotenssit eivät ole aivan ongelmattomia; varomaton laskeminen voi johtaa ristiriitoihin. Potenssiinkorotussääntökään ei ole rajoituksitta voimassa. Esimerkiksi laskussa

iⁱ = (cos + i sin )ⁱ = (e^i/2)ⁱ = e^-/2

voitaisiin myös kirjoittaa i = cos + i sin 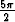, mikä johtaisi eri tulokseen!

kompleksiluku  imaginaariyksikkö  Eulerin kaava  sini  kosini

Kivelä, niinkuin matematiikka, versio 1.12