![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Integraali
Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ]
Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT:
![[#]](kuvat/msam10-c-4.gif) integraalifunktio,
integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali,
määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt
derivointisäännöt
KATSO MYÖS:
![[#]](kuvat/msam10-c-4.gif) Kansisivu Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto Hakemisto |
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät Sisällön pääryhmät  Integraali Integraali  Integroimistekniikkaa [ 1 2 3
4 5 ] Integroimistekniikkaa [ 1 2 3
4 5 ]
ESITIEDOT: ![[#]](kuvat/msam10-c-4.gif) integraalifunktio, integraalifunktio, ![[#]](kuvat/msam10-c-4.gif) määrätty integraali, määrätty integraali, ![[#]](kuvat/msam10-c-4.gif) derivointisäännöt derivointisäännöt
KATSO MYÖS: |
|
Toinen tärkeä menettely integraalien laskemisessa on osittaisintegrointi. Tätäkin
voidaan käyttää sekä integraalifunktion etsimiseen että määrättyjen integraalien
laskemiseen. Perustana on tulon derivoimiskaava kirjoitettuna muotoon
u'v = 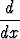 (uv) - uv'. Integroimalla tämä saadaan osittaisintegroinnin kaavat
(uv) - uv'. Integroimalla tämä saadaan osittaisintegroinnin kaavat
 u'(x)v(x) dx u'(x)v(x) dx | = | u(x)v(x) -  u(x)v'(x) dx, u(x)v'(x) dx, | ||
 u'(x)v(x) dx u'(x)v(x) dx | = |   u(x)v(x) - u(x)v(x) -  u(x)v'(x) dx. u(x)v'(x) dx. |
 u'v integraaliksi
u'v integraaliksi  uv' sekä
integraalia sisältämättömäksi lisätermiksi. Kaavoja sovellettaessa on alkuperäinen
integroitava funktio tulkittava funktioiden u' ja v tuloksi siten, että muunnettu
integraali on muodostettavissa, ts. funktio u (jonka derivaatta u' tunnetaan)
voidaan helposti laskea. Lisäksi tavoitteena tietenkin on, että muunnettu
integraali olisi yksinkertaisempi.
uv' sekä
integraalia sisältämättömäksi lisätermiksi. Kaavoja sovellettaessa on alkuperäinen
integroitava funktio tulkittava funktioiden u' ja v tuloksi siten, että muunnettu
integraali on muodostettavissa, ts. funktio u (jonka derivaatta u' tunnetaan)
voidaan helposti laskea. Lisäksi tavoitteena tietenkin on, että muunnettu
integraali olisi yksinkertaisempi.
![[#]](kuvat/msam10-c-4.gif) integraalifunktio integraalifunktio![[#]](kuvat/msam10-c-4.gif) määrätty integraali määrätty integraali![[#]](kuvat/msam10-c-4.gif) derivaatta (tulon) derivaatta (tulon) |
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12