Sisällön pääryhmät Integraali Määrätty integraali [ 1 2 3 4 5 6 7 8 ] ESITIEDOT:  summa ja tulo,  integraalifunktio KATSO MYÖS:  integroimistekniikkaa

Kansisivu  Sisältö  Hakemisto

Olkoon annettuna suljetulla välillä [a, b] määritelty reaaliarvoinen funktio f. Tämän ei tarvitse olla derivoituva eikä edes jatkuva. Jaetaan väli [a, b] osaväleihin jakopisteillä x_k, joille pätee

a = x₀ < x₁ < x₂ < ... < x_n = b.

Osavälejä on tällöin n kappaletta. Niiden pituuksia merkitään x_k = x_k - x_k-1; osavälien ei tarvitse olla yhtä pitkiä. Olkoon v_k jokin k:nnen osavälin piste: v_k [x_k-1, x_k]. Funktion f arvoista välillä [a, b] muodostettua summaa

f(v_k)x_k

kutsutaan Riemannin summaksi.

Lisätään jakopisteiden määrää välin [a, b] jaossa siten, että pisteiden määrän kasvaessa pisimmänkin osavälin pituus lähestyy nollaa. (Tämä merkitsee jaon tihentämistä tietyssä mielessä tasaisesti, so. suurin piirtein samalla tavoin välin eri osissa.) Tällöin vastaavassa Riemannin summassa n 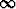ja x_k 0, ts. termien lukumäärä kasvaa, mutta samalla jokainen yksittäinen termi lähestyy nollaa. Ei ole selvää, miten Riemannin summa tällöin käyttäytyy: kumpi voittaa, äärettömyyteen vievä termien lukumäärä vai nollaan vievä yksittäisten termien suuruus.

Jos Riemannin summalla edellä kuvatussa rajaprosessissa on raja-arvo riippumatta siitä, miten pisteet v_k osaväleiltä valitaan ja miten jaon tasainen tihentäminen tapahtuu, sanotaan, että funktio f on integroituva välillä [a, b] ja sen määrätty integraali on mainittu raja-arvo. Merkitään

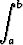f(x) dx = lim 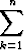f(v_k)x_k.

Rajaprosessi on luonteeltaan erilainen kuin lukujonon tai funktion raja-arvo. Itse asiassa määrätyn integraalin täsmällinen määrittely edellyttäisi tämänkin raja-arvotyypin määrittelyä 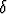- -tekniikalla.

Voidaan osoittaa, että jos f on jatkuva funktio, niin Riemannin summan raja-arvo on olemassa. Se on olemassa myös monille epäjatkuville funktioille, mutta ei kaikille.

Integraalien käyttö perustuu usein Riemannin summien mukaiseen ajatteluun, kuten seuraavat esimerkit osoittavat.

suljettu väli  funktio (reaali-)  derivoituvuus  jatkuvuus  alkio  summamerkintä  raja-arvo (lukujonon)  raja-arvo (funktion)

Kivelä, niinkuin matematiikka, versio 1.12