| linair.mws |
Airyn differentiaaliyhtälö on hyvin yksinkertainen toisen kertaluvun lineaarinen ja homogeeninen differentiaaliyhtälö, joka kuitenkaan ei ole ratkaistavissa tavallisten alkeisfunktioiden avulla:
> airyyht:= diff(y(x), x, x)-x*y(x)=0;
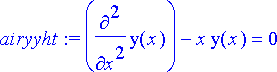
> ylrtk:= dsolve(airyyht, y(x));
Maple tuntee kuitenkin laajemman kokoelman funktioita, ja näiden avulla voidaan lausua sekä differentiaaliyhtälön yleinen ratkaisu että sen derivaatta.
> diff(ylrtk,x);
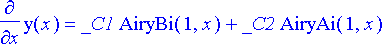
Kaksi lineaarisesti riippumatonta yksittäisratkaisua saadaan antamalla sopivat alkuehdot ja ratkaisemalla näistä vakiot. Aluksi yleinen ratkaisu määritellään funktioksi.
> airy:= unapply(rhs(ylrtk), x);
> vakiot:= solve({airy(0)=1, D(airy)(0)=0}, {_C1, _C2});
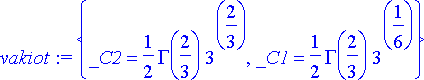
> vakiot2:= solve({airy(0)=0, D(airy)(0)=1}, {_C1, _C2});
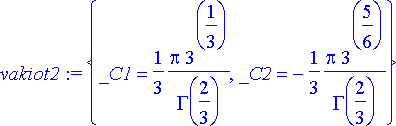
Saadut lausekkeet sisältävät uuden erikoisfunktion, gammafunktion. Tälle käytetään yleensä symbolia
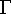(kreikkalainen kirjain iso gamma).
Vakioita vastaavat yksittäisratkaisut ovat
> rtk1:= subs(vakiot, airy(x));
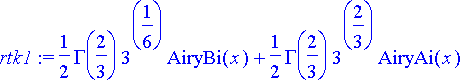
> rtk2:= subs(vakiot2, airy(x));
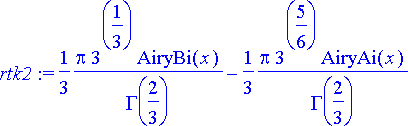
Näiden kuvaajista on nähtävissä eräitä toisen kertaluvun homogeeniyhtälölle luonteenomaisia piirteitä:
> plot({rtk1, rtk2}, x=-15..2);
![[Maple Plot]](Images/linair10.gif)
Jos differentiaaliyhtälössä
y
'' +
ky
= 0 vakio
k
on positiivinen, kyseessä on vakiokertoiminen yhtälö, jonka ratkaisuna on
![y = C[1]*sin(sqrt(k))*x+C[2]*cos(sqrt(k))*x](Images/linair11.gif)
, ts. sini-kosini-värähtely. Värähtelyn taajuus on sitä suurempi, mitä suurempi
k
on. Negatiivisilla muuttujan
x
arvoilla Airyn yhtälö on tämäntyyppinen: Yhtälö voidaan kirjoittaa muotoon
y
'' + |
x
|
y
= 0, ja sen ratkaisuna näyttää olevan värähtely, jonka taajuus kasvaa, kun |
x
| kasvaa.
Vastaavalla tavalla Airyn yhtälö voidaan rinnastaa positiivisilla muuttujan arvoilla yhtälöön
y
'' -
ky
= 0, missä
k
on positiivinen. Tämän ratkaisut muodostuvat eksponenttifunktioista:
![y = C[1]*exp(sqrt(k)*x)+C[2]*exp(-sqrt(k)*x)](Images/linair12.gif)
.
Kuvaajat näyttävät myös toisen kertaluvun homogeeniyhtälöiden ratkaisuille tyypillisen ominaisuuden: Jos kahdella lineaarisesti riippumattomalla ratkaisulla on nollakohtia, nämä vuorottelevat. Toisen ratkaisun kahden peräkkäisen nollakohdan välissä on täsmälleen yksi toisen ratkaisun nollakohta. Todistus perustuu Wronskin determinantin ominaisuuksiin.