Sisällön pääryhmät Diskreettiä matematiikkaa Binomi- ja multinomikertoimet [ 1 2 3 4 ] ESITIEDOT: KATSO MYÖS:  polynomit,  lukumäärän laskeminen

Kansisivu  Sisältö  Hakemisto

Binomikertoimeksi kutsutaan lauseketta

= ,

missä n ja p ovat kokonaislukuja ja n > 0, 0 < p < n.

Kombinatoriselta kannalta kerroin osoittaa, miten monella tavalla n olion joukosta voidaan valita p oliota, ts. montako p-kombinaatiota n oliosta voidaan muodostaa.

Kertoimet esiintyvät myös binomikaavassa

(x + y)ⁿ = 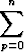x^n-py^p,

jonka avulla voidaan kehittää binomin x + y potenssit.

Näillä kahdella näkökulmalla on selvä yhteys. Binomin potenssi voidaan kirjoittaa

(x + y)ⁿ = (x + y)(x + y). . . (x + y),

missä tekijöitä x + y on siis n kappaletta.

Summien kertominen voidaan ajatella tapahtuvaksi siten, että poimitaan kaikilla mahdollisilla tavoilla jokaisesta tekijästä (x + y) aina yksi termi ja nämä kerrotaan keskenään; lopuksi saadut tulot lasketaan yhteen. Siten esimerkiksi tapauksessa n = 3 saadaan xxx + xxy + xyx + xyy + yxx + yxy + yyx + yyy. Yleisesti termejä on 2ⁿ kappaletta.

Termeissä on kuitenkin samanmuotoisia, jotka voidaan yhdistää. Edellä oleva lauseke saa tällöin muodon x³ + 3x²y + 3xy² + y³. Yleisessä tapauksessa muotoa x^py^n-p olevien termien lukumäärä ratkeaa sen mukaan, monellako tavalla n tekijästä (x + y) voidaan poimia ne p kappaletta, joista valitaan termiksi x; muista valitaan termiksi y. Kombinaatiotarkastelujen perusteella näiden lukumäärä on juuri , jolloin päädytään binomikaavaan.

binomikerroin  binomikerroin  kombinaatio  binomikaava  binomikaava  binomi  termi  lukumäärä (merkkijonojen)  lukumäärä (merkkijonojen)

Kivelä, niinkuin matematiikka, versio 1.12