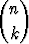Binomikaava
Binomikaava antaa binomin x + y potenssin kehitettynä:
(x + y)n = 
 xn-kyk, n = 1, 2, 3, ... .
xn-kyk, n = 1, 2, 3, ... .
Lausekkeen kertoimia
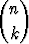 =
= 
kutsutaan binomikertoimiksi; tässä n! = 1 . 2 . 3 . ... . n on n-kertoma.
Binomikertoimet saadaan myös Pascalin kolmiosta. Binomikaava antaa
esimerkiksi
| (x + y)2 | = | x2 + 2xy + y2, | | |
| (x + y)3 | = | x3 + 3x2y + 3xy2 + y3, | | |
| (x - y)6 | = | x6 - 6x5y + 15x4y2 - 20x3y3 + 15x2y4 - 6xy5 + y6. | | |
Viimeisessä tapauksessa lauseke on ensin ajateltava muotoon (x + (-y))6.
Binomikaavan yleistyksenä on multinomikaava
(x1 + x2 + ... + xm)n = 
 x
x x
x ...x
...x ,
,
joka antaa vastaavalla tavalla multinomin x1 + x2 + ... + xm potenssit
kehitettyinä.
Kivelä,  niinkuin matematiikka, versio 1.12
niinkuin matematiikka, versio 1.12
![[#]](kuvat/msam10-c-4.gif) Sisällön pääryhmät
Sisällön pääryhmät  Potenssit ja polynomit
Potenssit ja polynomit  Polynomit [ 1 2 3
4 ]
Polynomit [ 1 2 3
4 ]
![[#]](kuvat/msam10-c-4.gif) summa ja tulo
summa ja tulo
![[#]](kuvat/msam10-c-4.gif) potenssi,
potenssi, ![[#]](kuvat/msam10-c-4.gif) polynomien tekijöihin jako,
polynomien tekijöihin jako, ![[#]](kuvat/msam10-c-4.gif) polynomiyhtälöt,
polynomiyhtälöt,
![[#]](kuvat/msam10-c-4.gif) binomi- ja multinomikertoimet,
binomi- ja multinomikertoimet, ![[#]](kuvat/msam10-c-4.gif) reaalifunktiot
reaalifunktiot
![[#]](kuvat/msam10-c-4.gif) Kansisivu
Kansisivu
![[#]](kuvat/msam10-c-4.gif) Sisältö
Sisältö
![[#]](kuvat/msam10-c-4.gif) Hakemisto
Hakemisto